どーも、ほーたです。
今回は超重要事項を解説していきます。
これは僕が受験生の頃からずっと大事にしていたことです。
何だと思いますか?
結論から言いますと、『作図』です。
作図を適当にやる受験生はそれ相応の成績しか取れません。
物理を勉強する上で欠けてはいけない要素です。
応用問題が全然出来ないという人もこれを意識する事から始めるといいでしょう。
基本問題から応用問題を解く上で非常に重要になってくることです。
それでは解説していきます。
目次
物理の問題を解く上で一番大切なのは作図
物理の基本問題を解く時にも、応用問題を解く時でも一番大切なのは作図です。
当たり前すぎますよね。でもこれがホントに大事です。
例えると、作図をしないで問題を解くことは、正規分の計算問題で途中式を書かないことくらい大切です。
積分の問題で途中式を書かないと絶対に計算ミスりませんか?
もしくは、頭がごっちゃになって計算なんて出来ないじゃないですか。
逆に途中式を書けば解ける問題は結構ありますよね。
作図をしないという事は計算問題で暗算をしているようなものです。
暗算をしなくなると次は物理現象のイメージが出来るようになります。
作図を丁寧にすることで圧倒的に物理現象はイメージできる
作図をする事で頭の中でイメージしようとしていた物理現象を視覚的にイメージできます。
物理という学問は身の回りの現象を数式に表すというものなので、その現象を目で見れるようにするという事は基本中の基本です。
例えば、
『物体が速度\(v\)で、床に対して斜めに入射します。そして、反発係数\(e\)で跳ね返りました。床はなめらかとする。』という文章と下図、どちらが状況を把握しやすいですか?
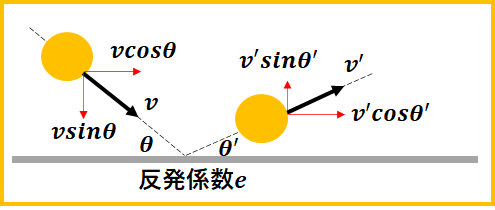
当然、図を見たほうが状況を把握しやすいですよね。
速度を分解して図に書き込むと、さらに分かりやすくなりますよね。
物理現象を頭でイメージする事よりも目で見える状態にするって大事だと思いませんか?
状況把握ができると使うべき公式がわかりやすくなる
さて、状況を把握できましたね。
そうすると使うべき公式が分かるようになります。
床とは反発係数\(e\)で跳ね返るので、鉛直方向について反発係数の公式が使えます。
$$e=\frac{v’sin\theta’}{v\sin\theta}$$
そして、水平方向については、外力が働かないので運動量保存が成り立ちます。
$$mv\cos\theta=mv’\sin\theta’$$
実際に運動を目で理解できると爆発的に公式が立てやすくなります。
つまり、作図は公式を立てるための途中式のようなものです。
僕は試験の時はすべて丁寧な作図をしていた
僕は普段の勉強からこの作図をかなり丁寧にしていました。
問題文を読んだら、解き方を思いついても、まずは作図を書くという事を徹底していました。
そうすることで模試の時や実際の試験の時にも作図する事が癖になります。
だから、試験で緊張している時でも体が勝手に作図をしてくれます。
もう体で覚えているレベルで沁みついてましたねww
体で覚えているレベルで作図する癖が身に着いていると、
視覚的なイメージから問題を考えることが出来るので圧倒的に解くのが楽になりますよ。
問題文を読んだら即作図は鉄則!作図を癖にする!
作図をする癖をつけて問題を解けるようにするにはやるべきことは2つです。
- 簡単な基本問題でも作図をしてから問題を解く
- 図を書いて物理量を書き込む
たったこれだけです。
今日この後物理の勉強する時にこの2点を意識して問題を解くようにして下さい。
オッケーですか?
運動や状況を視覚的にイメージすることが物理を武器にする一歩目です。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<


