どーも、ほーたです。
自分が大学受験の時を思い返してみると
『例題や基本問題は解けるけど、問題のレベルが上がると全然解けなくなる。。。』
という事に悩んでいました。
過去の僕と同じく、
このような悩みを持っている方は何がいけないのでしょうか??
『基本問題→応用問題』という一見正しいように思えるこのやり方、
実は大きな間違いがあります。
今回はそれについて解説していきます。
目次
応用問題を解けるようになるための3ステップ
基本問題は解けるのに応用問題が解けないという人は、学習到達度によっり大きく3つの段階に分かれています。
まず、第一段階は「基本問題の解き方を覚えているだけで、なぜそうなるかを理解していない」という人。
そして、第二段階は「なぜそうなるかは理解できていても、教科書の理解が不十分」である人。
最後に、第三段階は「教科書の内容を理解しているものの、応用問題を解く訓練が不足している」という人。
では、それぞれについて説明していきます。
第一段階「基本問題の解き方を覚えているだけで、なぜそうなるかを理解していない」
これは、模試で(1)は解けるけど、それ以降全く分からないという人が該当します。
いわゆる、「見たことのある問題しか解けない」人です。もっと言うと、公式の理解が出来ていない人です。
例えば、なめらかな水平面上で運動している2物体が衝突するときに運動量保存が成り立つ、という事を表面的に覚えてしまい、なぜ運動量保存則が成立するかを理解していないという事です。
こういう方は、まず基本問題で正解する事ではなく、基本問題でなぜその解き方になるか?という事を理解する事に努めましょう。
もう一度念押ししますが、「こういう問題はこの公式を使えばいい」とは考えないでください。
そういう人は絶対に伸びませんので。
第二段階「なぜそうなるかは理解できていても、教科書の理解が不十分」
次に、少しステップアップした問題が解けなくなる人です。
この段階の人はかなり多くみられます。
言い換えると、「少し複雑になると本質が見えなくなる人」です。
例えば、次のような問題を考えましょう。
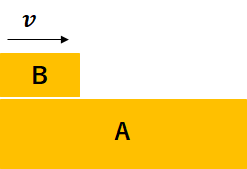
図のように、なめらかな水平面上の質量\(M\)の物体Aの上で質量\(m\)の物体Bを初速度\(v\)で滑らせる。すると、物体Bだけでなく物体Aも動き出した。物体Aと物体Bの間には摩擦が働くとし、動摩擦係数を\(\mu’\)として、次の問いに答えよ。
- 物体Bが物体A上で速度が\(v’\)になった時の物体Aの速度を求めよ。
- 物体Bはやがて物体A上で静止するとします。2つの物体が合体して運動するまでの物体Aと物体Bの運動について論ぜよ。
(1)番は簡単でしょう。
上に運動量保存と書いていたので、解けた人がいたかもしれません。
でも、それで運動量保存と思いつくのは第一段階と同じになります。
物体Aと物体Bの間には内力のみで、外力が働いでいない
↓
運動量保存が成り立つ
という思考が出来ればナイスです。
$$\begin{eqnarray*}& &mv+M\times 0=mv’+MV’\\\\\Longleftrightarrow& &v’=\frac{m}{M}(v-v’)\end{eqnarray*}$$
問題は(2)ですね。
これが出来れば基本的な物理力があってもいいでしょう。
論じ方は人それぞれですが、自分の力で説明できるようになることが大切です。
まずは力の作図をしてみて下さい。そうすると、物体Aには右向き、物体Bには左向きに動摩擦力が働きます。(左:Bについて、右:Aについて)
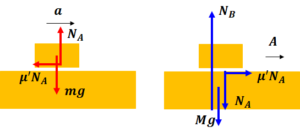
運動方程式を立てましょう。
$$\begin{eqnarray*}& &A \ : \ MA=\mu’ mg\\\\& &B \ : \ ma=-\mu’ mg\end{eqnarray*}&&
つまり、物体Aは右向きに加速度\(\displaystyle A=\frac{m}{M}\mu’ g\)を受けて等加速度直線運動をして、物体Bは左向きに加速度\(a=-\mu’ g\)を受けて等加速度運動をします。
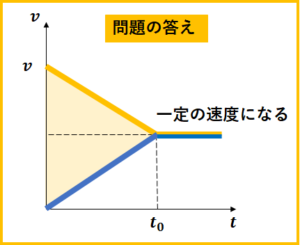
物体Aは加速し、物体Bは減速するので、物体Bが物体Aで運動している時は、2つの物体が同じ速度になるタイミングがあります。そこで、物体Bが物体A上で静止するというわけです。
静止するまでの物体Aと物体Bの速度を等加速度運動の公式で表してみましょう。物体Aは、初速度\(0\)で加速度\(\displaystyle\frac{m}{M}\mu’ g\)で、物体Bは初速度\(v\)で加速度\(-\mu’ g\)なので、
$$\begin{eqnarray*}& &v_{A}=v-\mu’ gt\\\\& &v_{B}=\frac{m}{M}\mu’ gt\end{eqnarray*}$$
\(v-t\)グラフは次のようになります。
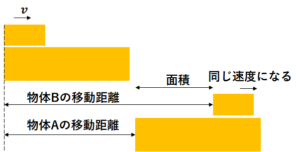
また、運動の前後の図は次のようになります。
ここで言いたいのは、「なぜ?」を追求してほしいという事です。
気になる箇所があれば必ず解決するようにしましょう。
第三段階「教科書の内容を理解しているものの、応用問題を解く訓練が不足している」
そして、最後に応用問題の訓練不足です。
正直第二段階までこれたらここからは、伸びるだけだと思っています。偏差値65までは絶対に行けるでしょう。
今までにつけた基礎力の応用の仕方を学んで、応用問題にどんどん取り組むことが大切です。
解けなかった場合はなぜ解けなかったのか?
どの単元の応用だったのか?
をしっかり分析して、次にどのように対処すればいいかを考えましょう。
共通して大切なのは『どの基本事項が応用されているか?』
以上の3ステップを説明しましたが、どれにも共通して大切なのが
『どの基本事項が応用されているか?』
という事です。
これはどういうことかと言いますと、斜方投射を考えてみればわかります。
斜方投射って
- 水平方向に等速直線運動
- 鉛直方向に鉛直投げ上げ運動
の運動をしますよね。
つまり、斜方投射は等速直線運動と鉛直投げ上げ運動の応用問題という事になります。
もっと応用問題を見てみましょうか。
例えば一定の速度で上昇する気球で斜方投射をするときはどのような運動になるでしょうか?
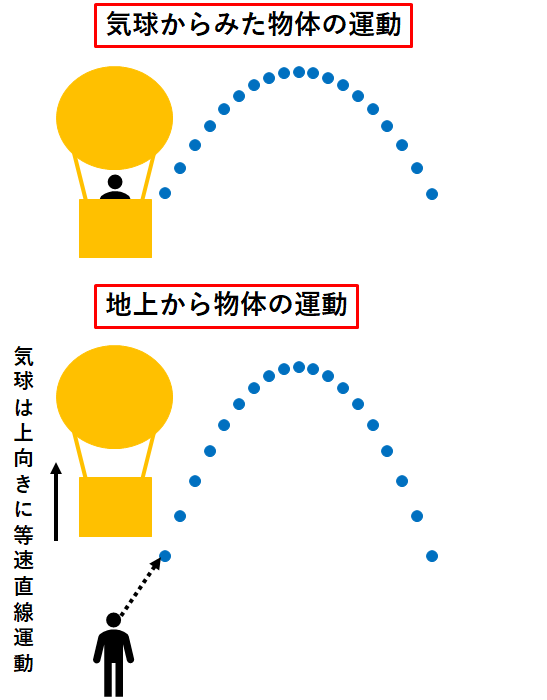
図を見れば大体わかりますが、計算方法も簡単です。
- 気球に乗って物体の運動を見たら斜方投射運動
- 地上から見た気球の運動は鉛直上向きに等速直線運動
- 地上から見た物体の運動は「(気球の運動)+(気球から見た物体の運動(斜方投射))」の合成(合成速度)
つまり、この問題は鉛直投げ上げ運動と等速直線運動と合成速度の3つが応用されている問題になります。
このように「この問題は何が応用されているのか?」を考えて演習を積むことが大切です。
教科書を大切に
ここまで第三段階まで書きましたが、個人的に一番大切にするべきは教科書です。
大学入試は教科書さえできれば解けるようにできています。
ですが、その教科書を疎かにする人が非常に多く、勿体ないです。
物理の根本は教科書に詰まっており、教科書をは反復して人に説明できるようになれば問題なく、応用問題も解けるようになります。
公式だけでなく、教科書の文章にも目を通して、「なぜ?」を追求して基礎固めをしましょう。
まとめ
このまとめを見て、記事の内容を説明できるまで反復しましょう。
応用問題を解けるようにする3ステップ
-
基本問題の解き方を覚えているだけで、なぜそうなるかを理解していない
-
なぜそうなるかは理解できていても、教科書の理解が不十分
-
教科書の内容を理解しているものの、応用問題を解く訓練が不足している
大切なのは、1番と2番。
教科書を理解して理解を深めるべし。
それでは。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<


