運動方程式の立て方！2つのポイントをまとめました！

こんにちは、ほーたです。

今回は運動方程式の立て方について解説したいと思います。

これは前回の『ニュートンの運動方程式とは？？京大生がわかりやすく解説します』と同様、力学では最も大切な部分です。

必ず理解するようにしてください。

運動方程式２ポイント

運動方程式の2つのポイントです。

これを次の具体例で解説していきます。

【具体例】

角度\(\theta\)の斜面上に質量\(M\)の物体Aがのっている。物体と斜面に摩擦力がない時の物体Aの運動方程式をたてよ。

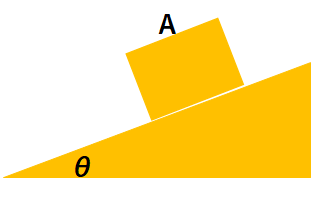
力の作図

力の作図のポイントは４つあります。

1. メインの物体を決める
2. 力の正の方向を決める
3. 力の作図(接触力、場による力)
4. x,y成分に分ける

順番に説明していきます。

メインの物体を決める

これから力を書こうとしてる物体を決めます。

今回は物体Aについての力の作図です。

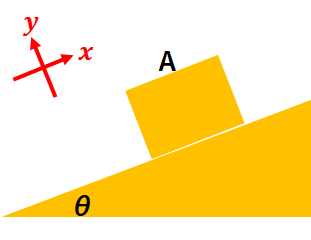
力の正の方向を決める

力の正の方向を決めます。

これはx軸とy軸の向きを決めるということです。

こうすることで運動方程式を立てる際に計算ミスが減ります。

この正の向きは正解がなく、ミスをなくすために設定するというイメージです。

力の作図(接触力、場による力)

まず、力は接触力と場による力があります。

接触力・・・ほかの物体と接触している点から受ける力。

張力、垂直抗力、摩擦、弾性力、圧力、浮力など

場による力・・・物体が場によって受ける力。接触していが物体にかかる力。

重力場、磁場や電場による力。

これをそれぞれで探して作図していきます。

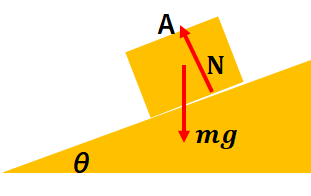
x、y成分に分ける

力をxとy方向に分解します。

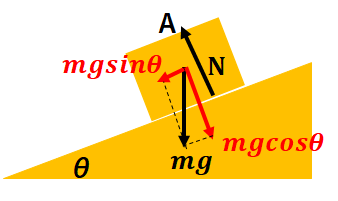
x軸とy軸について運動方程式を立てる

x軸とy軸方向それぞれで運動方程式を立てていきます。

加速度をxとy軸方向に分解しましょう。

これをそれぞれ\(a_{x}\)と\(a_{y}\)とします。

作図した図を見ながら運動方程式を立てましょう。

$$x : M a_{x}=-M g \sin\theta$$

$$y : M a_{y}=N-M g \cos\theta$$

今回の場合は\(a_{y}=0\)なので

$$x : M a_{x}=-M g \sin\theta$$

$$y : 0=N-M g \cos\theta$$

となります。

この手順で運動方程式を立てれば計算ミスも少なくなり、正確に問題を解くことが出来ます。

少し難しい問題で演習してみましょう

それでは問題演習をしていきましょう。

適当に解かれない様に難しめにしました。

必ず上記の2ポイントを大切にしてください。

問題

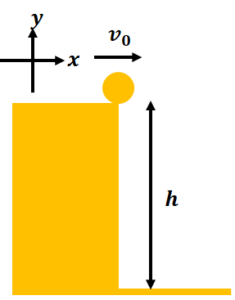
空気抵抗がある中での質量\(m\)のボールを水平投射をする。図のように高さ\(h\)のところから水平方向に速度\(v_{0}\)でボールを投げます。重力加速度を\(g\)とします。空気抵抗はボールの進行方向と逆向き働き、大きさは速度に比例し大きさ\(k v\)を受けるものとする。ボールについての運動方程式を立てなさい。ただし、x軸とy軸は図のようにとり、xとy方向の加速度をそれぞれ\(a_{x}\)と\(a_{y}\)、xとy方向の速度をそれぞれ\(v_{x}\)と\(v_{y}\)とします。

解答

これを感覚的に解こうとすると解けない人が多く出ると思います。物理力がかなりないと感覚的には解けません。力の作図をして運動方程式の手順をしっかり守りましょう。

１．力の作図

１．注目する物体を決める

ここでは注目する物体はボールです。

２．力の正の方向を決める

問題文に指定された通りのx軸とy軸に従います。

３．力の作図（場の力、接触力）

ここでは場の力が重力、接触力が空気抵抗です。

向き注意して作図します。

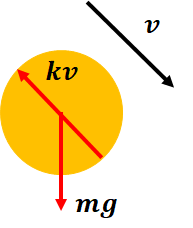
４．力をxとyに分解する

作図した力をx軸とy軸方向に分解します。

今回は空気抵抗がx方向、y方向にそれぞれ\(k v_{x}\)、\(k v_{y}\)に分解されます。

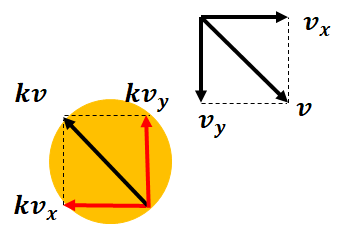
２．x軸とy軸方向の運動方程式を立てます。

作図した通りに運動方程式を立ててください。

$$m a_{x}=-k v_{x}$$

$$m a_{y}=-mg+k v_{y}$$

ちなみにこの運動の軌道は下図のようになります。

このグラフは高さ10 mから速度100 kmで水平投射したときの軌道です。

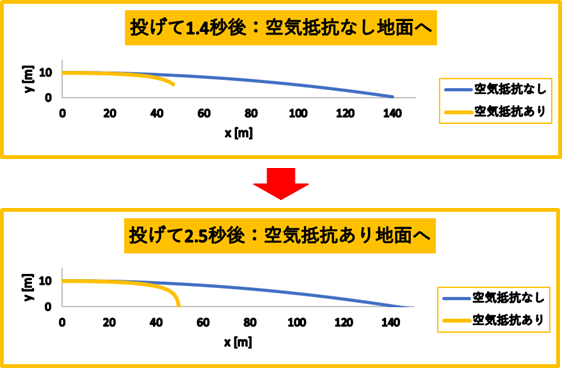
参考として青線で空気抵抗のない時の水平投射の軌道も載せておきます。

このグラフを見ると分かりますが、空気抵抗がない方が地面に落下するまでの時間が、空気抵抗があるときよりも、1秒ほど早く、飛ぶ距離が100 mほど遠くに飛んでいますね。

オレンジの軌道を見ればわかりますが、空気抵抗ありの方は50 mのあたりから垂直に落ちています。

これは空気抵抗によってボールの水平方向の速度が0まで減速されていることが分かります。

また空気抵抗があるとy軸方向の落下速度も徐々に一定になっていきます。

この一定になる速度を終端速度といいます。

このグラフはy軸方向の速度の大きさと時間の関係ですが\(t=2\)の時以降一定になってることが分かります。

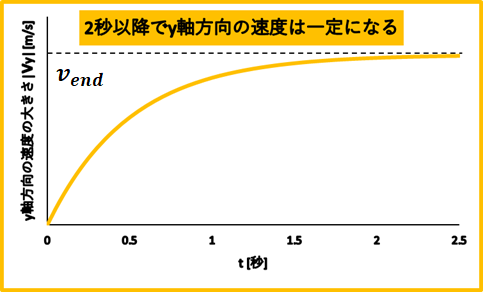
この時の速度は加速度\(a_{y}=0\)なのでy軸方向の運動方程式から終端速度\(v_{end}\)は

$$v_{end}=-\frac{m g}{k}$$

と求まります。

まとめ

いかがでしたでしょうか。

運動方程式は型通り解けば必ず立てれるので、このパターンを必ず覚えていてください。

そして空気抵抗がある場合の水平投射の問題は難しいと思う方も多いと思いますが、大学入試当日には出来るようにしてください。

いつも言いますが、分からなければ反復して音読し、しっかりと理解するようにしてください。

オリジナルテキストを無料でプレゼントします

僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。

しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。

その一番のきっかけになったのを力学の考え方にまとめました。

力学の基本中の基本です。

色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。

無料配布中です。

もしくは、下記画像をクリック！