こんにちは、ほーたです。
今回は、弾性力による位置エネルギーについて解説していきます。
位置エネルギーのイメージとしては、重力による位置エネルギーが強いと思いますが、弾性力の位置エネルギーもあります。
重力による位置エネルギーと違い、弾性力による位置エネルギーは力が一定ではないので、エネルギーの証明方法が異なります。
公式の証明はかなり大切になるので、必ず理解するようにして下さい。
弾性力の位置エネルギーについて学ぶために、「仕事の考え方」と「運動エネルギー」について理解してることが望ましいので、下記から勉強してください。
【合わせて読みたい】
仕事の考え方
→仕事で注意するべきポイントと仕事率についてわかりやすく解説します
運動エネルギー
→運動エネルギーとは??公式の求め方から具体的な計算まで詳しく解説します
弾性力による位置エネルギーを理解し、最重要の公式の証明を身に着ける。
目次
弾性力による位置エネルギーとは
弾性力による位置エネルギー
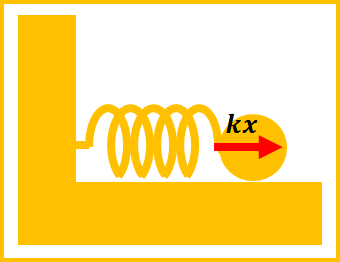
フックの法則により、\(x\)だけ伸びた、または、縮んだばねからは力\(k\times x\)が働きます。
図のようにばねにボールをつけておくと、力の働く方向にボールが加速することになります。
これは、ばねがボールに仕事をすることで、ボールにエネルギーを与えたということです。
つまり、伸びたり縮んだりするばねはエネルギーを持ち、それがボールの運動エネルギーに変換されます。
そのばねが持つエネルギーを弾性力による位置エネルギー\(U_{k}\)[J]といいます。
弾性力による位置エネルギーの公式とその求め方
弾性力とは??
そもそも弾性力って何??と思う方も多いと思います。
詳しくは、下記の記事に書いているので、こちらをお読みください。
フックの法則やばね定数についても勉強できるので合わせて勉強しましょう。
【合わせて読みたい】
弾性力について
→フックの法則とばね定数についてわかりやすく解説します
弾性力による位置エネルギーの公式
弾性力の位置エネルギーは、ばね定数\(k\)に比例し、ばねの伸び、または、縮み\(x\)の2乗に比例します。
$$U_{k}=\frac{1}{2}k x^2$$
公式からわかるように、弾性力による位置エネルギーは、重力による位置エネルギーと違い、常に正の値をとります。
弾性力による位置エネルギーの公式の求め方
それでは公式を証明していきます。
この証明方法は、かなり大切なので、必ず出来るようにして下さい。
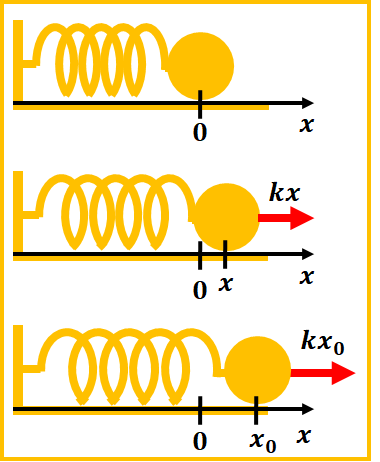
図のように、ばねを通常状態から\(x_{0}\)伸ばす時を考えます。この時に加える力は、ばねの力と釣り合うように加えるとします。
そして、ばねに加える力以外に力は働いてないとします。
まず、求める位置エネルギーを\(U_{k}\)、ばねにした仕事を\(W\)とすると、仕事をした分位置エネルギーに変わるので、
$$U_{k}=W$$
となります。
ここで、仕事のポイントを確認しましょう。
- 正の向きを決める
- 移動方向と垂直の力は仕事していない
- 力が一定でない場合は\(F\)-\(x\)グラフの面積から求める
正の向きは、図の右方向、力はばねの伸びる方向と同じ方向になり、加える力は\(F=k\times x\)となるので一定ではない、ここからばねにする仕事\(W\)は、\(F\)-\(x\)グラフの面積から求めることになります。
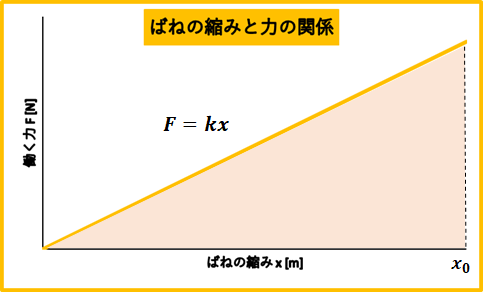
図のグラフの面積がばねにする仕事なので、面積を求めると
$$W=\frac{1}{2}k x_{0}^2$$
と求まります。
これは、弾性力による位置エネルギー\(U_{k}\)と等しくなります。
$$U_{k}=\frac{1}{2}k x_{0}^2$$
弾性力による位置エネルギーと運動エネルギーの関係
ばねに質量\(m\)のボールをつけて、弾性力による位置エネルギーとボール運動エネルギーの関係を見ていきましょう。
物体をそっと離す場合

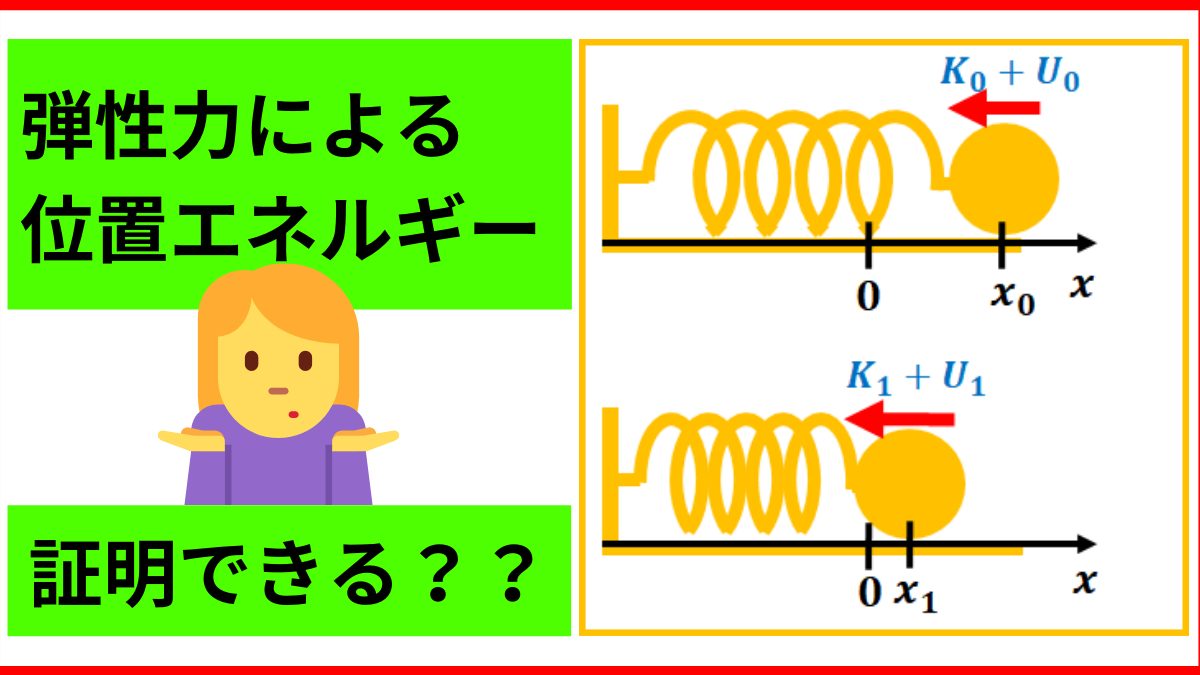
図のように、ばねが\(x_{0}\)だけ伸びている状態でボールを離す、この時の運動を考えましょう。
ボールの座標が\(x_{1}\)になるときのボールの運動エネルギー\(K_{1}\)を求めていきましょう。
まず、ボールの座標が\(x_{1}\)の時のボールの運動エネルギー\(K_{1}\)は、\(x_{0}\)から\(x_{1}\)になるまでに、ばねがボールにした仕事\(W_{1}\)になります。
$$K_{1}=W_{1}$$
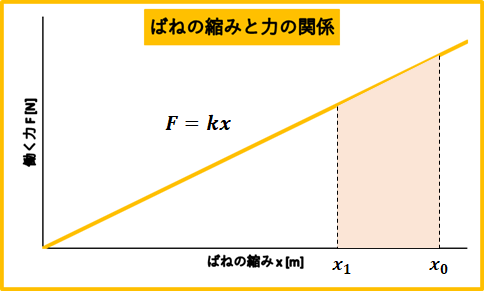
つまり、図の台形の面積になります。
その面積\(W_{1}\)は、
$$W_{1}=\frac{1}{2}k(x_{0}^2-x_{1}^2)$$
と表せますね。
また、ボールの座標が\(x_{1}\)の時の、ばねの位置エネルギー\(U_{k 1}\)は
$$U_{k 1}=\frac{1}{2}kx_{1}^2$$
となります。
座標\(x_{1}\)の時の、ボールの運動エネルギー\(K_{1}\)と弾性力による位置エネルギー\(U_{k 1}\)の和を求めると、
$$\begin{align}K_{1}+U_{k 1}=&W_{1}+U_{k 1}\\\\=&\frac{1}{2}k(x_{0}^2-x_{1}^2)+\frac{1}{2}kx_{1}^2\\\\=&\frac{1}{2}kx_{0}^2\end{align}$$
ここから、ボールの運動エネルギーとばねの位置エネルギーは常に等しいということが分かります。
物体に初速度を与える場合
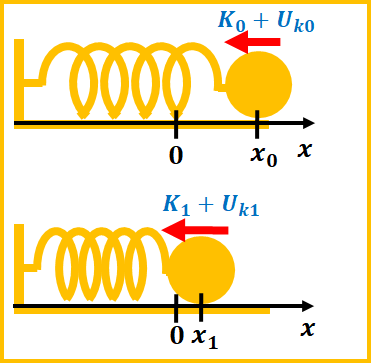
次は、ばねが\(x_{0}\)だけ伸びた状態から初速度\(-v_{0}\)(図の左向きに速さ\(v_{0}\))で投げたときの運動を考えましょう。
こちらでも、ボールの位置が\(x_{1}\)の時のボールの運動エネルギー\(K_{1}\)を求めます。
まず、ボールに初速度を与えたときの運動エネルギー\(K_{0}\)と位置エネルギー\(U_{k 0}\)の和は、
$$K_{0}+U_{k 0}=\frac{1}{2}mv_{0}+\frac{1}{2}kx_{0}^2$$
になります。
結論から言うと、ボールの座標が\(x_{1}\)のときの運動エネルギーと位置エネルギーの和は等しくなります。
これを示していきましょう。
ボールの座標が\(x_{1}\)の時のボールの運動エネルギー\(K_{1}\)は、\(x_{0}\)から\(x_{1}\)になるまでにばねがボールにした仕事\(W_{1}\)と最初の運動エネルギー\(K_{0}\)の和になります。
$$K_{1}=W_{1}+K_{0}$$
\(W_{1}\)、\(U_{k 1}\)に関しては、上記の求め方と同じで、
$$\begin{align}W_{1}=&\frac{1}{2}k(x_{0}^2-x_{1}^2)\\\\U_{k 1}=&\frac{1}{2}k x_{1}^2\end{align}$$
となります。
よって、ボールの座標が\(x_{1}\)の時の運動エネルギー\(K_{1}\)と位置エネルギー\(U_{k 1}\)の和は、
$$\begin{align}K_{1}+U_{k 1}=&(W_{1}+K_{0})+U_{k 1}\\\\=&\{\frac{1}{2}k(x_{0}^2-x_{1}^2)+\frac{1}{2}mv_{0}^2\}+\frac{1}{2}k x_{1}^2\\\\=&\frac{1}{2}k x_{0}^2+\frac{1}{2}m v_{0}^2\\\\=&K_{0}+U_{k 0}\end{align}$$
となります。
これで証明出来ました。
まとめ
今回は弾性力による位置エネルギーの公式、その求め方、運動エネルギーとの関係を解説しました。
公式の導出、運動エネルギーを求める時の考え方は超重要なのでかならず身に着けるようにして下さい。
また、下記に重力による位置エネルギーについて、力学的エネルギーの保存について解説しているので、しっかり学習して仕事とエネルギーをマスターしてください。
【合わせて読みたい】
重力による位置エネルギー
→重力による位置エネルギーとは??公式や運動エネルギーとの関係をわかりやすく解説します
力学的エネルギー保存則
→力学的エネルギー保存則とは??公式や仕事との関係までわかりやすく解説します
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<