こんにちは、ほーたです。
今回は重力による位置エネルギーについて解説しようと思います。
初心者でも簡単に理解できるように書いたので最後まで読んでください。
この記事をよく前に、「仕事の考え方」と「運動エネルギーについて」を勉強することをおススメします。
【合わせて読みたい】
仕事の考え方
→仕事で注意するべきポイントと仕事率についてわかりやすく解説します
運動エネルギー
→運動エネルギーとは??公式の求め方から具体的な計算まで詳しく解説します
重力による位置エネルギーを公式の証明から理解する。
目次
重力による位置エネルギーとは
重力による位置エネルギーとは
スマホを足に落としたとき、めちゃくちゃ痛いですよね。
さらにそれが、広辞苑だったらもっと痛いですよね。
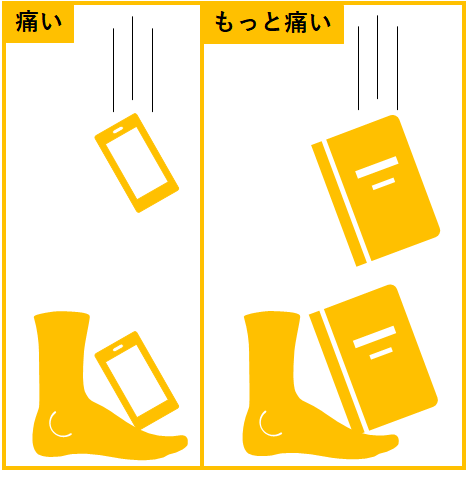
このように、重くて、高い位置にある物体はエネルギーを持ち、そのエネルギーを位置エネルギーといいます。
重力による位置エネルギーの公式とその求め方
重力による位置エネルギーの公式
位置エネルギーの公式
位置エネルギー\(U_{g}\)は物体の質量\(m\)と基準地点からの高さ\(h\)に比例します。
$$U_{g}=mg\times h$$
基準値の高さとは
ここで注意してほしいのが、高さ\(h\)は地上からの高さではなく、基準地点からの高さということです。
この基準地点からの高さとは、その地点の位置エネルギーを0とし、そこから物体の位置エネルギーを求めるということになります。
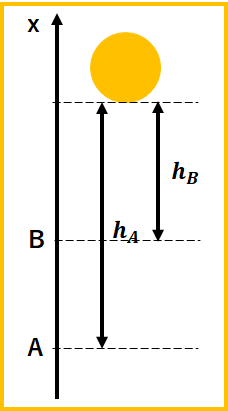
例えば、図のように地点Aを基準にすれば、地点Aから物体までの高さは\(h_{A}\)となり、位置エネルギー\(U_{g A}\)は、\(U_{g A}=mg\times h_{A}\)となります。
また、地点Bを基準地点にすれば、地点Bから物体までの高さは\(h_{B}\)となり、位置エネルギー\(U_{g B}\)は、\(U_{g B}=mg\times h_{B}\)となります。
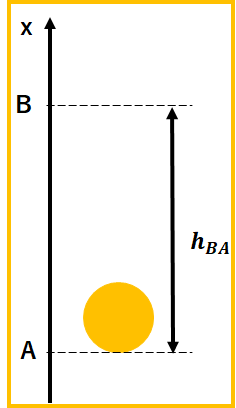
また、この図のように、地点Aに物体があるときの地点Bを基準地点としたときの位置エネルギー\(U_{g BA}\)を求めると、
$$U_{g BA}=-mg h_{BA}$$
となります。
基準地点によっては、位置エネルギーが負の値になることがあるので要注意です。
つまり、基準点より低ければ重力の位置エネルギーは負の値をとる、ということに要注意です。
それでは公式をまとめます。
$$U_{g}=mgh$$
\(h\) : 基準地点からの高さ
重力による位置エネルギーの公式の求め方
それでは公式\(U_{g}=mgh\)を求めていきましょう。
図のように、地面を基準地点としてとり、そこから高さ\(h\)まで、等速直線運動になるように運びます。
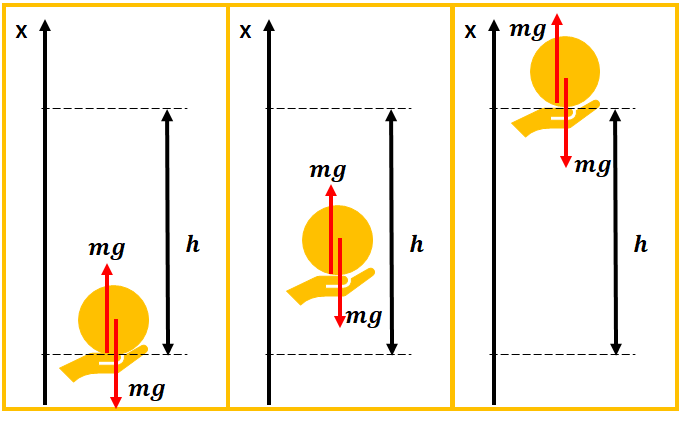
つまり、物体に常に力\(F=mg\)を加えながら高さ\(h\)まで運ぶということですね。
この時に、持ち上げる時に要した仕事\(W\)が位置エネルギー\(U_{g}\)と同じになります。
仕事のポイントを復習しましょう。
- 正の向きを決める
- 移動方向と垂直の力は仕事しない
- 力が変化する場合は、\(F\)-\(x\)グラフの面積から求める
今回は正の向きを上向きとし、力は一定で移動方向と同じ向きに働くので、持ち上げる時に要した仕事\(W\)は、
$$W=mg\times h$$
となり、位置エネルギーと等しくなることが分かります。
重力による位置エネルギーと運動エネルギーの関係
それでは位置エネルギーと運動エネルギーの関係を、次の二つの場合に分けて考えてみましょう。
物体を自由落下させる場合
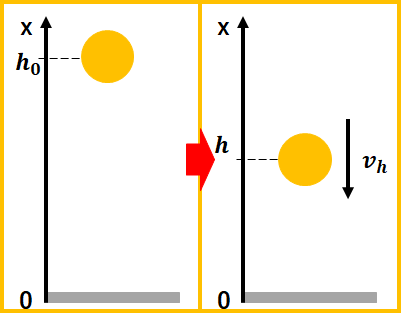
図のように高さ\(h_{0}\)から質量\(m\)の物体を自由落下する状態を考えてみましょう。
基準地点を地面としたときの最初の状態では位置エネルギー\(U_{g}\)は、
$$U_{g}=m g h_{0}$$
になります。
そして、上向きを正の向きとしたときの等加速度運動の公式を求めると、初期位置\(h_{0}\)、初速度\(0\)、加速度\(-g\)なので、
$$v=-gt$$
$$x=h-\frac{1}{2}gt^2$$
となり、そうすると、高さ\(h(<h_{0})\)の時の物体の速度\(v_{h}\)を求めると、
$$v_{h}=-\sqrt{2(h_{0}-h)g}$$
となります。
この時の運動エネルギー\(K_{h}\)を求めると、
$$K_{h}=\frac{1}{2}m v_{h}^2=mg(h_{0}-h)$$
となって、さらに、この時の位置エネルギー\(U_{g h}\)は、
$$U_{g h}=mg h$$
となるので、高さ\(h\)の時の運動エネルギーと位置エネルギーの和は、
$$K_{h}+U_{g h}={mg(h_{0}-h)+mg h}=mg h_{0}$$
となります。
ここから、運動エネルギーと位置エネルギーの総和は同じになることが分かります。
また、高さが低くなった分位置エネルギーが運動エネルギーに変わった、ということが分かります。
これが分からない方や等加速度運動の考え方をまだ勉強してない方、運動エネルギーを勉強していない方は下記から勉強してください。
【合わせて読みたい】
等加速度運動の考え方
運動エネルギー
→運動エネルギーとは??公式の求め方から具体的な計算まで詳しく解説します
物体を斜方投射をする場合
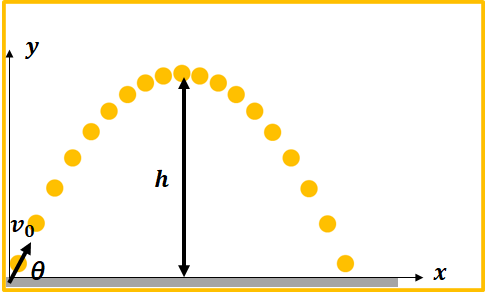
次は、少しレベルを上げて、質量\(m\)の物体を角度\(\theta\)、初速度\(v_{0}\)で斜方投射する状況を考えていきましょう。
今回も基準地点は地面とし、上向きをy軸の正の方向、右向きにx軸の正の方向として、等加速度運動の公式を求めます。
x軸方向の速度 : \(v_{x}=v_{0}cos \theta\)
x軸方向の位置 : \(x=(v_{0}cos \theta)t\)
y軸方向の速度 : \(v_{y}=v_{0}sin\theta-gt\)
y軸方向の位置 : \(y=(v_{0}sin\theta)t-\frac{1}{2}gt^2 \)
ここの求め方が分からない方は、下記の斜方投射の記事から勉強してください。
【合わせて読みたい】
斜方投射の考え方
→放物運動の斜方投射とは??公式や導出などわかりやすく解説します
放物線の最高点を\(h\)とすると、上記の等加速度運動の公式から、
$$h=\frac{v_{0}^2 sin^2 \theta}{2g}$$
となります。
この時水平方向の速度が\(v_{0}cos \theta\)なので、最高点でのエネルギー\(E\)は
$$E=mgh+\frac{1}{2}m (v_{0}cos \theta)^2=\frac{1}{2}mv_{0}^2$$
となります。
ここで、最初のエネルギーは運動エネルギーだけなので、そのエネルギー\(K_{0}\)は、
$$K_{0}=\frac{1}{2}m v_{0}^2$$
となり、運動エネルギーと位置エネルギーの和が同じになることが分かります。
また、物体の高さが高くなるにつれて運動エネルギーが位置エネルギーに変化してることが分かります。
まとめ
今回の位置エネルギーで大切なのは、公式\(mgh\)を覚えると同時に、高さが基準地点からの高さということになります。
これを注意して重力による位置エネルギーを扱うようにして下さい。
また、下記に弾性力による位置エネルギーについて、力学的エネルギーの保存について解説しているので、しかっり勉強してください。
【合わせて読みたい】
弾性力による位置エネルギー
→弾性力による位置エネルギーとは??公式や運動エネルギーとの関係をわかりやすく解説します
力学的エネルギー保存
→力学的エネルギー保存則とは??公式や仕事との関係をわかりやすく解説します
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<