こんにちは、ほーたです。
今回は斜方投射について。
考え方は水平投射と同じです。
だから水平投射を勉強した人にはよゆーですね。
初めての方はしっかり勉強して、今日マスターしてしましょう。
これを読む前に加速度運動の考え方と運動の独立性、放物運動の考え方の記事を読んでから、こちらを読むのをお勧めします。
【合わせて読みたい】
等加速度運動の考え方
運動の独立性、放物運動の考え方
→放物運動の水平投射とは??公式や導出などわかりやすく解説します
公式を覚えずとも運動の独立性をもちいて、斜方投射の問題を扱えるようになる。
目次
斜方投射
斜方投射運動とは物体を斜めに投げる運動のことをいいます。
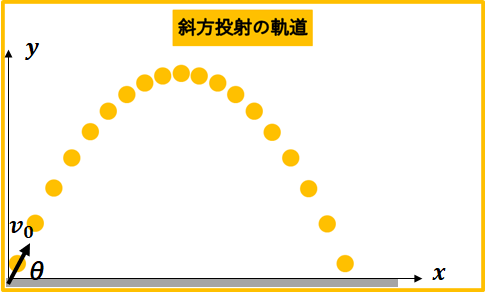
この運動も放物運動の考え方に従って、
- 軸を決定する
- 運動の独立性
- 初期位置、初速度、加速度
の順に考えていきます。
図のようにx軸とy軸をとり(軸の決定)、運動の独立性からxとy成分に分けて(運動の独立性)、初期位置、初速度、加速度を求める(初期条件)。

さっそく公式の証明からいきます。
斜方投射の公式
等加速度運動の公式から斜方投射の速度と位置の公式を求めます。
x軸について
$$\begin{align}v_{x}=&v_{0}\cos\theta\\\\x=&(v_{0}\cos\theta)t\end{align}$$
と求まり、
そしてy軸は
$$\begin{align}v_{y}=&v_{0}\sin\theta-gt\\\\y=&(v_{0}\sin\theta)t-\frac{1}{2}gt^2\end{align}$$
と求まります。
これの式からx軸には等速直線運動、y軸には鉛直投げ上げ運動をしていることが分かりますね。
こういうところで、今まで勉強してきた基礎が応用されています。
こうやって公式が導ければ、暗記量が少なくても物理の問題に対応することが出来ます。
x軸
速度 : \(v_{x}=v_{0}\cos\theta\)
位置 : \(x=(v_{0}\cos\theta)t\)
y軸
速度 : \(v=v_{y}=v_{0}\sin\theta-gt\)
位置 : \(y=(v_{0}\sin\theta)t-\frac{1}{2}gt^2\)
斜方投射の軌道を見る
では斜方投射の位置の公式から\(t\)を消去して\(y\)を求めます。
xの位置の式より、
$$t=\frac{x}{v_{0}\cos\theta}$$
と求まる。これをyの位置の公式に代入します。
$$\begin{align}y=&(v_{0}\sin\theta)\frac{x}{v_{0}\cos\theta}-\frac{1}{2}g(\frac{x}{v_{0}\cos\theta})^2\\\\=&x\frac{\sin\theta}{\cos\theta}-\frac{1}{2}g\frac{x^2}{v_{0}^2}\frac{1}{\cos^2\theta}\\\\=&-\frac{1}{2}g\frac{1}{v_{0}^2\cos^2\theta}(x-\frac{v_{0}^2\sin2\theta}{2g})^2+\frac{v_{0}^2\sin^2\theta}{2g}\end{align}$$
最後は平方完成しただけです。
これをy-xグラフ図示。
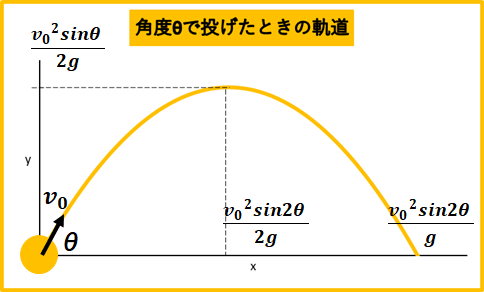
また落下したとき、
x軸方向の速度は\(v_{0}\cos\theta\)となり、
y軸方向の速度は鉛直投げ上げ運動の運動の対称性から\(-v_{0}\sin\theta\)となるので、
速度を合成すると落下するときの速さは\(v_{0}\)になります。
これから、斜方投射は、\(x=\frac{v_{0}^2sin2\theta}{2g}\)を中心に対称な運動をしていることが分かりました。
練習問題
それではここで問題を解いてみましょう。
【問題】
野球ボールを水平から\(\theta\)の角度で投げた。空気抵抗を無視でき、さらにボールの大きさを無視できる場合どの角度でボールを投げれば落下したときに水平距離にして一番遠くに飛ぶか。
【解答】
ボールが飛んだ距離は先ほど求めました。
$$y=x\frac{\sin\theta}{\cos\theta}-\frac{1}{2}g\frac{x^2}{v_{0}^2}\frac{1}{\cos^2\theta}$$
において、\(y=0\)を満たす\(x\)が飛距離あたります。
だから、飛距離\(x_{1}\)は
$$x_{1}=\frac{2v_{0}^2\sin\theta\cos\theta}{g}$$
となります。ここで二倍角の公式\(\sin2\theta=2\sin\theta\cos\theta\)を用いて\(x_{1}\)を変形すると
$$x_{1}=\frac{v_{0}^2\sin2\theta}{g}$$
となります。
この\(x_{1}\)が最大になる角度は\(\theta=45\)の時なので、
飛距離が最大になるのは\(\theta=45\)になります。
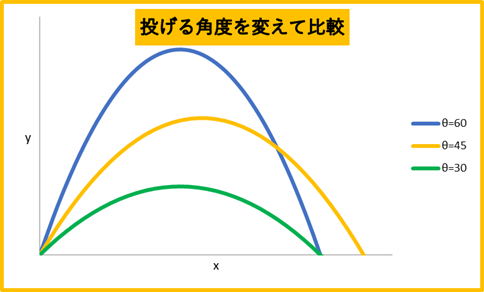
参考までに\(\theta\)を30、45、60の軌道をプロットしました。
45の時が一番飛距離がわかりますね。
【終】
まとめ
このまとめを見て、記事の内容を説明できるまで反復しましょう。
斜方投射の公式
x軸
速度 : \(v_{x}=v_{0}\cos\theta\)
位置 : \(x=(v_{0}\cos\theta)t\)
y軸
速度 : \(v=v_{y}=v_{0}\sin\theta-gt\)
位置 : \(y=(v_{0}\sin\theta)t-\frac{1}{2}gt^2\)
それでは。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<