こんにちは、ほーたです。
物理を勉強して初めて習う現象の等加速度運動と等速直線運動。
なかなか物理に慣れていない方は、理解が難しかったりしていきなり挫折!なんてこともあるかもしれません。
ですが、理解してしまえばそこまで難しいことではないですし、実際つまずく人も多いので心配ありません。
しっかり理解できるように詳しく説明してます。
これは物理全般で大事になる内容なので、根気よく理解することが大切。
それでは解説していきます。
等速直線運動と等加速度運動を理解し、公式の導出が出来るようになる。
目次
【超重要】軸の決定
等加速度運動の公式を求める前にまず軸の決定について説明します。
これを知ることで公式を覚える量が圧倒的に減るので、しっかり身に着けてください。
軸の決定とは等加速度運動の公式において初期位置を決めること、初速度と加速度の正負を決めることに重要です。
ここで初速度はスタートの速度のことをいいます。
軸を決めたときの物体の位置座標を初期位置とし、初速度と加速度の向きは、軸の向きと同じならば正、逆向きならば負とする癖をつけましょう。
簡単な話x軸とy軸を設定しようということです。
そうすれば原点も決まるし、向きの正負も決まります。
軸の決め方には正解はないので、問題集の解答と違っても問題ありません。
1.物体の初期位置
2.物体の初速度の正負
3.物体の加速度の正負
等速直線運動と公式の導出
さて、まずは等速直線運動の説明から。
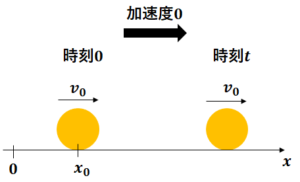
等速直線運動は文字通り「等しい速度の直線運動」といいます。
時間がたった後の物体の速度や位置は公式として表せます。
これを導いていきましょう。
等速直線運動の公式の導出
上の図のように初期位置\(x_{0}\)、初速度\(v_{0}\)となるように\(x\)軸をとります。
等加速度運動の速度の公式は、初速度\(v_{0}\)のまま同じ速度で直線運動をしてるから、
$$v=v_{0}$$
と表されることが分かります。
速度というのは単位時間1秒当たりの変位の変化なので、\(t\)秒たった後に進んだ移動距離\(x_{1}\)は、速度に時間\(t\)をかければいいです。
というわけで、移動距離は、
$$x_{1}=v_{0}t$$
そうすると等速直線運動の公式は最初の位置も考慮して
(\(t\)秒後の位置)=(初期位置)+(移動距離)
なります。それを文字を使って表すと
$$x=x_{0}+v_{0}t$$
と導かれます。
速度 : \(v=v_{0}\)
位置 : \(x=x_{0}+v_{0}t\)
ここまでは簡単。
等加速度運動の公式の証明はちょいとムズイですが、
大切だからしっかり理解しましょう。
等加速度運動と公式の導出
等加速度運動とは「等しい加速度の運動」のことをいいます。
これは一定の加速度で運動してるということです。
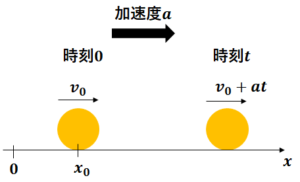
速度と位置で公式を導いていきます。
等加速度運動の公式の導出
上の図のように初期位置\(x_{0}\)、初速度\(v_{0}\)、加速度\(a\)となるように\(x\)軸をとります。
t秒後の速度を求める
加速度とは一秒間に速度がどれくらい変化したかです。
だから、一秒間に速度\(v_{0}\)が\(v_{0}+a\)に加速される、という事です。
つまりは
(\(t\)秒後の速度)=(最初の速度)+(加速した分)
となります。それを文字に直すと以下のようになります。
$$v=v_{0}+at$$
これが等加速度運動の時の速度の式です。
ここまでは、等速直線運動と同じ考え方ですが、位置の証明がややこしい。
t秒後の位置を求める
続いては位置の公式を求めていきます。
ここで加速度運動においてめちゃくちゃ大事なポイントがあります。
これを抑えましょう。
\(v\)-\(t\)グラフの傾きは加速度、面積は移動距離。
\(v=v_{0}+at\)をグラフにすると下図の感じです。
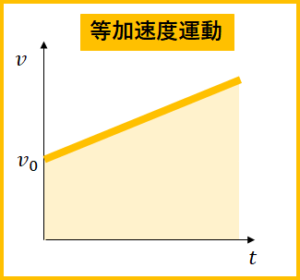
傾きは自明だが、面積が移動距離になる理由はあとで説明するとして、このポイントを使い公式を求めていきます。
面積を求めると移動距離\(x_{1}\)は、
$$x_{1}=v_{0}t+\frac{1}{2}gt^2$$
となります。
求める位置は(初期位置+移動距離)から\(x_{0}+x_{1}\)となるので
$$x=x_{0}+v_{0}t+\frac{1}{2}gt^2$$
が得られます。
これが位置の公式。
位置と速度の式からもう一つ
そして求めた式からもう一つ公式を導きます。
$$v=v_{0}+at$$
$$x=x_{0}+v_{0}t+\frac{1}{2}at^2$$
この二つの式から\(t\)を消去。
すると次の公式が得られます。
$$v^2-v_{0}^2=2a(x-x_{0})$$
これが三つ目の公式。
以上が等加速度運動の公式です。
速度 : \(v=v_{0}+a t\)
位置 : \(x=x_{0}+v_{0}t+\frac{1}{2}at^2\)
\(t\)を消去 : \(v^2-v_{0}^2=2a(x-x_{0})\)
これで\(a=0\)の時が等速直線運動。
つまり等速直線運動は等加速度運動の一部になります。
公式が減った!楽やんー。
僕が高1の時、これを知ってこんなことを考えていました。
この感覚がマジで大事です。
バカ暗記するよりも覚える公式を減らしていきましょう。
このように覚える量を減らすことは物理では大切になります。
じゃあ、面積が移動距離になる理由を解説していきます。
分からなければ、何度も読んで理解して下さい。
\(v\)-\(t\)グラフの面積が移動距離になるわけ
等速直線運動の\(v\)-\(t\)グラフ
等速直線運動の移動距離の求め方は、
「速度というのは単位時間1秒当たりの変位の変化なので、\(t\)秒たった後に進んだ移動距離は速度に時間\(t\)をかければいい。」
でした。
つまり移動距離\(x_{1}\)は
$$x_{1}=v_{0}\times t$$
となります。
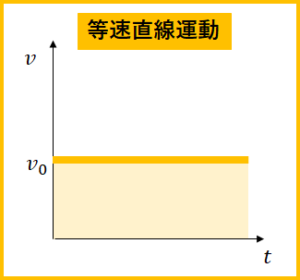
これは等速直線運動のグラフの面積と同じになります。
ここは簡単ですね。
理解できる人も多いと思います。
次に、この考え方をもちいて、
等加速度運動について考えていきます。
等加速度運動の\(v\)-\(t\)グラフ
等加速度運動の速度の公式は
$$v=v_{0}+at$$
でした。
なので、これの\(v\)-\(t\)グラフは下図。
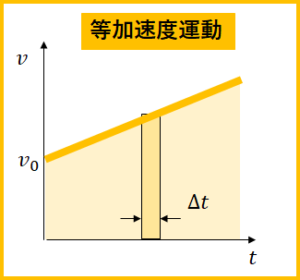
そして1つの長方形を考えます。
ここで、\(\Delta t\)は非常に小さいので、
この区間を等速直線運動していると近似すると、
長方形の面積は\(\Delta t\)秒間で移動した距離になります。
このような小さな時間に分割して、
それぞれを等速直線運動とみて、各微小時間での移動距離を足し合わせることで、
全体の移動距離が得られます。
これで等加速度運動の公式は完璧。
次は等加速度運動の問題を扱う上で大切な考え方を説明します。
等加速度運動の最強の考え方
等加速度運動の公式が分かったところで、
今後、等加速度運動の問題を解くうえで大切な考え方の解説です。
それは等加速度運動の問題を解くときには、必ず、
- 軸の決定
- 初期位置\(x_{0}\)、初速度\(v_{0}\)、加速度aを整理
の順番で考えて下さい!
例えば、初期位置が5、初速度が10 m/s、加速度が2 m/s²のときの等加速度運動の式は
$$v=10+2\times t$$
$$x=5+10\times t+\frac{1}{2}\times 2\times t^2$$
ですね。
こうすることで、暗記量が圧倒的に少なくなります。
この考え方は、ホントに大事だから、
絶対に出来るようにね。
まとめ
このまとめを見て、記事の内容を説明できるまで反復しましょう。
等加速度運動の公式
速度 : \(v=v_{0}+a t\)
位置 : \(x=x_{0}+v_{0}t+\frac{1}{2}at^2\)
\(t\)を消去 : \(v^2-v_{0}^2=2a(x-x_{0})\)
等加速度運動の考え方
1.正の向き
2.初期位置、初速度、加速度を求める
それでは。
【合わせて読みたい】
自由落下運動
鉛直投げ上げ
→鉛直投げ上げ運動とは??公式や導出まで分かりやすく解説します
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<