こんにちは、ほーたです。
水平投射。
ここから等加速度運動の考え方だけでは通用しなくなります。
でも簡単なので大丈夫です。
この記事を読めばしっかり理解できるように書きました。
それではさっそく解説していきます。
ただ、等加速度運動の考え方が分からな人は、
これを読む前に加速度運動の考え方の記事を読んでから、こちらを読むのをお勧めです。
【合わせて読みたい】
加速度運動の考え方
公式を覚えずとも運動の独立性を用いて、水平投射の問題を扱えるようになる。
目次
放物運動とは
曲線を描いて飛んでいく運動を放物運動といいます。
曲線を描いて飛ぶ、だとあまりイメージつかないかもしれないが、
放物線を描く運動だと思ってくれていいです。
よくやるキャッチボールの軌道、これも放物運動。
ああーこんな感じねー。程度の理解で大丈夫。
そしてこの放物線を描く運動は軌道のイメージが明確に出来ないため、
運動の独立性というものを用いて解析します。
これが、自由落下や鉛直投げ上げの時には考えなかったややこしいところです。
運動の独立性
運動の独立性とは、聞いただけだとすごく難しく感じるかもしれないが、単純にx軸とy軸の成分に分けるということです。
x方向とy方向それぞれで運動を見ることでより運動が見やすくなります。
それが最大のメリット。
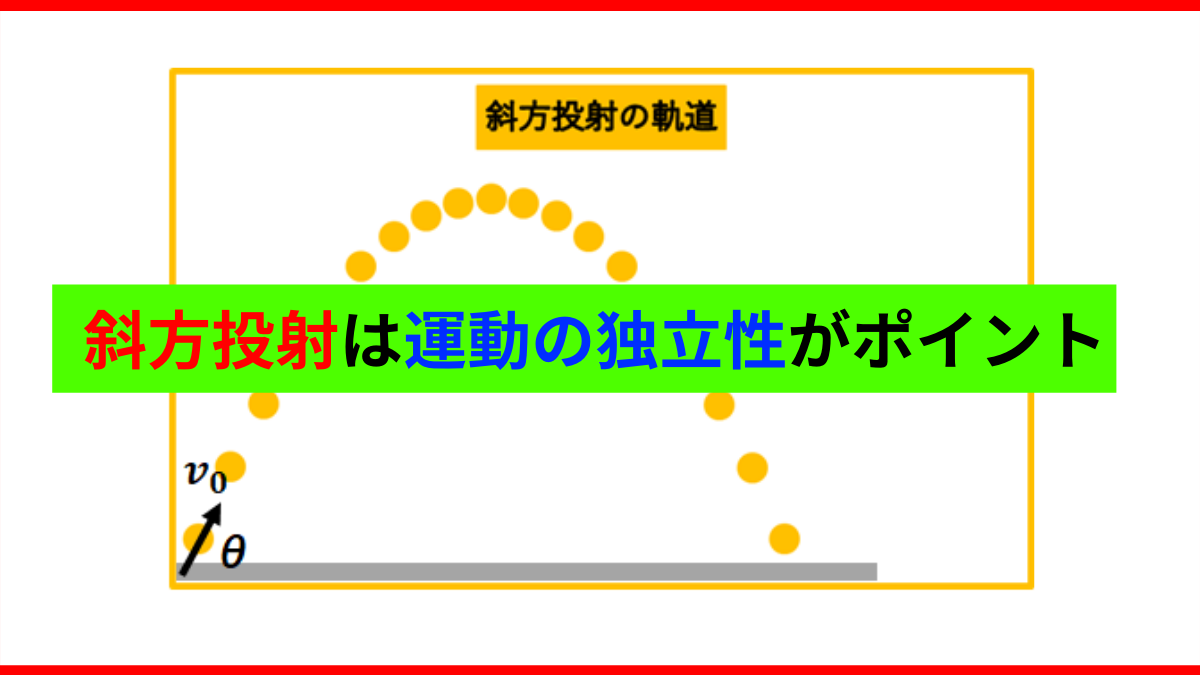
例えば、次のように物体を斜めに投げるときに水平と鉛直に分けることをいいます。
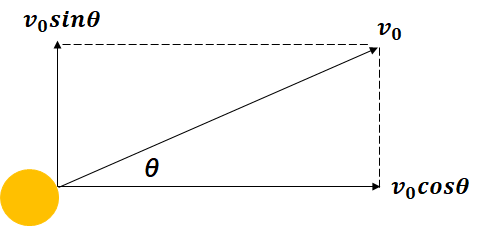
こうすることで、例えば、
x軸方向には、等速直線運動
y軸方向には、鉛直投げ上げ運動
をしているということが分かります。
少し工夫することで、今まで習ってきたことに帰着できます。
放物運動の考え方
放物運動は等加速度運動の考え方に加えて次のように考えるといいです。
- 軸の決定
- 運動の独立性
- 初期位置、初速度、加速度を求める
これに従って公式を導いていきます。
水平投射
水平投射運動とは水平に物体を投げたときの運動のことをいいます。
真横にボールを投げるだけ、こんなイメージですね。
今回は物体を投げる位置を原点として公式を導いていきます。
これが水平投射のイメージの図。
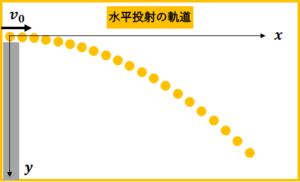
まず図のようにx軸とy軸をとります。(軸の決定)
この運動を運動の独立性を用いてx軸とy軸に分けて考えていきます。(運動の独立性)
運動の独立性から水平投射運動の各成分の初期位置、初速度、加速度は次の表のようになります。(初期条件を求める)

それを等加速度運動の公式に代入することで、
水平投射の公式が求められるというわけです。
水平投射の公式
ではx軸とy軸それぞれで速度と位置の公式と位置の公式を求めていきます。
x軸では表から
$$\begin{align}&v_{x}=v_{0}\\\\&x=v_{0}t\end{align}$$
次にy軸も同様に
$$\begin{align}&v_{y}=gt\\\\&_{y}=\frac{1}{2}gt^2\end{align}$$
と求められました。
式を見ればわかりやすいですね。
x軸方向には等速直線運動、y軸方向には自由落下運動になっています。
x軸
速度 : \(v_{x}=v_{0}\)
位置 : \(x=v_{0}t\)
y軸
速度 : \(v_{y}=gt\)
位置 : \(y=\frac{1}{2}gt^2\)
水平投射の運動を視覚的に見る
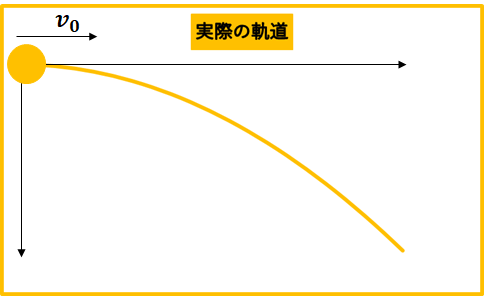
さて、ここでどのような軌道を描いているか実際に確認してみましょう。
水平投射の位置の式から\(t\)を消去。
そうすると
$$y=\frac{1}{2}\frac{g}{v_{0}^2}x^2$$
が得られます。
これは実際にどのような軌道で飛んでいるかを表している関数。
これをy-xグラフに図示すると次のようになります。
イメージ通りといえばイメージ通りですね。
なんか水平にボールを投げたらこういう軌道を描きそうです。
原点を頂点とした放物線を描きます。
問題演習で理解を深める
簡単な問題を解いて理解を深めましょう。
問題
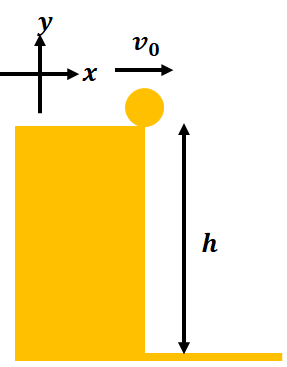
図のように高さ\(h\)から水平に初速度\(v_{0}\)で水平投射する。落下したときに水平距離でどれくらい飛んでいるか求めよ。ただし重力加速度を\(g\)とし、空気抵抗がないものとする。
解答
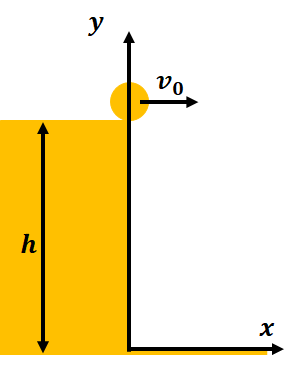
放物運動の考え方に従って問題を解く。図のように軸を設定し、運動の独立性から初期条件を求めます。

よって等加速度運動の式は以下の通りです。
x方向
$$\begin{align}&v_{x}=v_{0}\\\\&x=v_{0}t\end{align}$$
y方向
$$\begin{align}&v_{y}=-gt\\\\&y=h-\frac{1}{2}gt^2\end{align}$$
まず、落下したときの時間\(t_{0}\)は\(y=0\)の時なので、y方向の位置の式に代入して、
$$0=h-\frac{1}{2}gt_{0}^2$$
となるので、これから\(t_{0}\)を求めると、
$$t_{0}=\sqrt{\frac{2h}{g}}$$
となります。
よって水平方向の距離\(x_{1}\)は、
$$\begin{align}x_{1}=&v_{0}\times t_{0}\\\\=&v_{0}\sqrt{\frac{2h}{g}}\end{align}$$
と求まりました。
これの空気抵抗ありバージョンは下記で読めるので、是非読んでみて下さい。
空気抵抗があるだけでこれだけ軌道が変わるのか!!ってなります。
【合わせて読みたい】
空気抵抗ありの場合
まとめ
このまとめを見て、記事の内容を説明できるまで反復しましょう。
放物運動の考え方
1.軸の決定
2.運動の独立性
3.初期条件(初期位置、初速度、加速度)
水平投射の公式
x軸
速度 : \(v_{x}=v_{0}\)
位置 : \(x=v_{0}t\)
y軸
速度 : \(v_{y}=gt\)
位置 : \(y=\frac{1}{2}gt^2\)
それでは。
斜方投射についての記事も一緒に読むとより理解が深まります。
【合わせて読みたい】
放物運動の斜方投射とは??公式や導出などわかりやすく解説します
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<