こんにちは、ほーたです。
今回は慣性の法則と慣性力について解説していきます。
両方とも「慣性」がつきますが、なかな両方の意味がつながらないという方が多いと思うのでこの記事でしっかり理解してほしいと思います。
それでは解説していきますね。
慣性の法則と慣性力の関係を理解し、慣性力について例を交えて深く理解する。さらに、慣性系と非慣性系と使いこなす。
目次
慣性の法則とは??
水平面を滑っている物体を考えてみましょう。
その物体の運動は水平面の状態によって変わりますよね。
例えば道路のように表面が粗ければ、摩擦力を進行方向と逆向きに受けて、物体の速度は遅くなって最終的に静止し、スケートリンクのような表面が滑らかだと、力を受けないので、物体は同じ速度のまま運動します。
この物体が力を受けない、または、受けていても、力が釣り合っている時、物体はその速度を一定に保つ。
これを慣性の法則といいます。
力を受けていない、または、釣り合っている時に、物体は、静止し続ける、または、等速直線運動を続ける
電車の例から慣性の法則を理解する(電車外からの視点)
慣性の法則を考えるにあたり、観測者が電車の外から運動を眺めてる、という状態を考えます。
電車がブレーキをかけた時に、乗っている人たちは進行方向に引っ張られたり、または、電車内のつり革が進行方向に傾くことを確認できると思います。
人が進行方向に引っ張られたり、つり革が進行方向に傾くのは慣性の法則が働いているからです。
具体例で考えていきましょう。ここではつり革だけにフォーカスして考えていくとします。
これは次のようなイメージで考えると分かりやすいです。
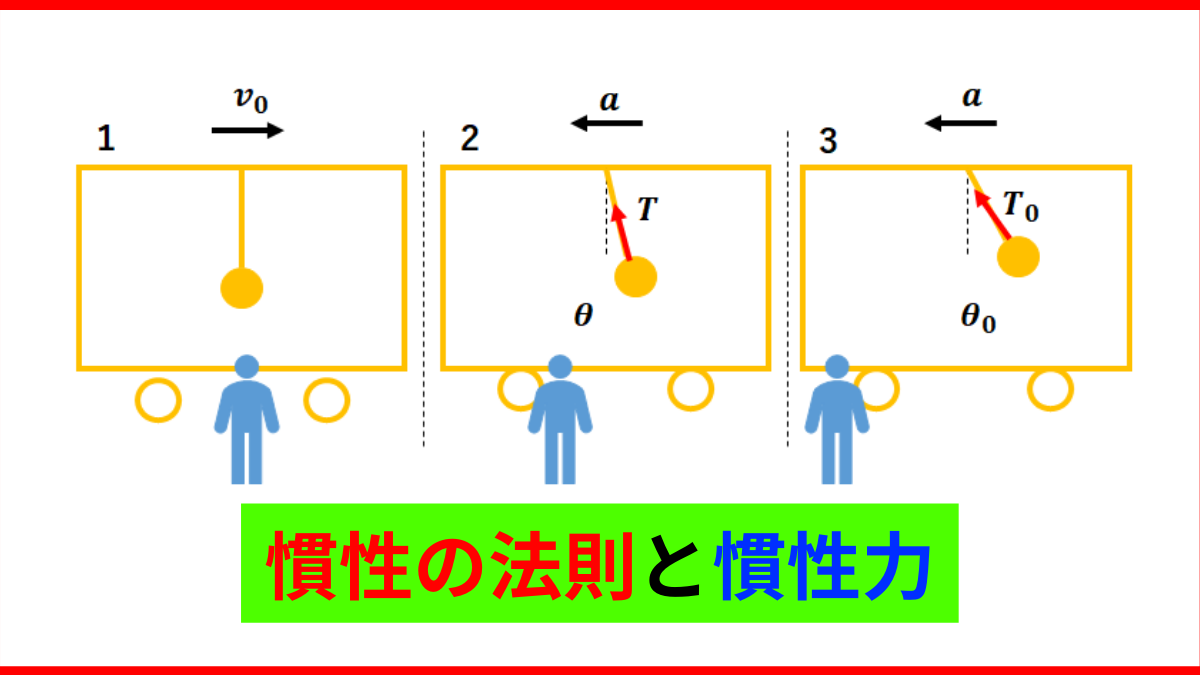
- 電車とつり革が速度\(v_{0}\)で運動してる。
- 電車がブレーキをかける。この時つり革は慣性の法則に従い速度\(v_{0}\)で等速直線運動をし続けようとする。故につり革は電車の進行方向に傾き始める。
- つり革の加速度が電車と同じ加速度(右向きに大きさ\(a\))になったところでそのまま電車と同じ運動をする。
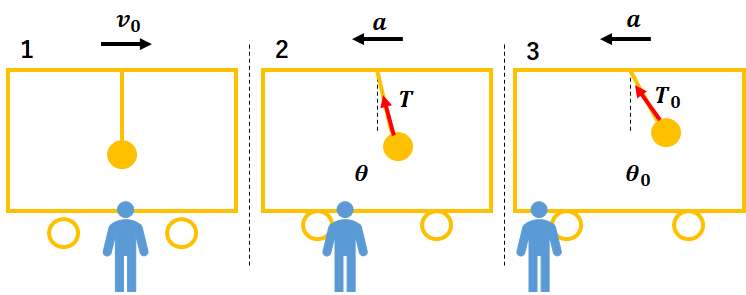
これを式的に理解していきましょう。
そこでつり革を軽い糸につるされた質量\(m\)のおもりと見立てて運動を考察していきます。
そしておもりの加速度が右向きに大きさ\(a\)になった時の角度を\(\theta_{0}\)、その時の張力を\(T_{0}\)とします。つまり、\(T(\theta_{0})=T_{0}\)ということです。
また電車が速度\(v_{0}\)からブレーキをかけるとします。
おもりの加速度の大きさが右向きに\(a\)になった時の、おもりについての運動方程式を立てていきましょう。
$$進行方向 : m(-a)=-T_{0}\sin\theta_{0}$$
もう一つの電車内での視点は次の慣性力で説明します。
慣性力とは??
電車の例から慣性力を理解する(電車内での視点)
次に慣性力を電車の中からの視点から理解していきましょう。
電車内での視点で見ると、電車がブレーキかけた時につり革が傾き始め、つり革の角度が\(\theta_{0}\)になった時に静止します。
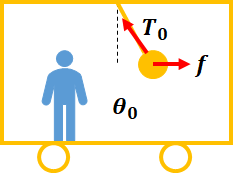
この時電車内からつり革を見るとつり革が静止してるように見えるので、水平方向で力のつり合いが成り立つはずです。
力のつり合いを立ててみましょう。
$$0=T\sin\theta_{0}$$
これは明らかにおかしいですね。
本来は左向きの力が働かないとおかしいので、その力を慣性力と名付け、大きさを\(f\)と仮定します。
それで力の作図をしましょう。
$$0=f-T\sin\theta_{0}$$
この式と電車外視点の運動方程式を比較すると
$$f=ma$$
なります。
慣性力の大きさは\(ma\)になります。
大地に対して加速度\(a\)で動く人から見える力で、加速度方向とは逆向きで、大きさ\(ma\)の力
見かけの重力加速度を使いこなす
そしてこの慣性力が働いているときには、見かけの重力加速度を考えることが出来ます。
これは慣性力と重力の合力を見かけの重力にするということです。
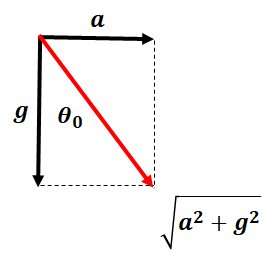
上記の電車の例の場合、下向きに重力、右向きに慣性力、そしてその合力が見かけの重力で、見かけの重力加速度\(g’\)は、
$$g’=\sqrt{g^2+a^2}$$
と表せます。
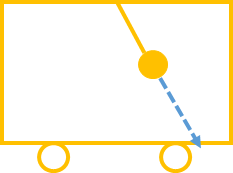
だから例えば、このブレーキをかけてる中で、つり革がちぎれたら、電車内ではこの見かけの重力加速度\(g’\)に従って自由落下運動をする、ということです。
$$v=-g’t$$
$$x=-\frac{1}{2}g’t^2$$
に従うということですね。
落下の軌道は図のようになります。
慣性系と非慣性系
慣性系
慣性系は、ニュートンの運動法則の第一法則と第二法則が成り立つ座標系になります。
つまり慣性の法則と運動方程式が成り立つ座標系のことです。
ここでいう座標系とは、視点だと思ってくれたら問題ありません。
上の電車の例でいうと電車外からの視点が慣性系になります。
非慣性系
非慣性系は、慣性系に「非」がついてるだけで、ニュートンの運動法則の第一法則と第二法則が成り立たない座標系のことをいいます。
電車の例でいうと、電車内での視点のことです。
慣性力が働く座標系が非慣性系ですね。
練習問題
一度エレベーターの問題で、二つの視点の理解を深めましょう。
【問題】
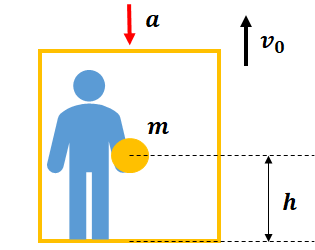
図のように下向きに加速度\(a\)で減速しているエレベーター内に人が乗っているとします。エレベーターの速度が\(v_{0}\)の時に、高さ\(h\)から質量\(m\)のボールを落としたときの、落下するまでの時間\(t_{0}\)をエレベーターの外と中の視点から求めてみましょう。重力加速度を\(g\)とする。
解答
それでは二つの視点で解いていきましょう。
エレベーターの外からの視点
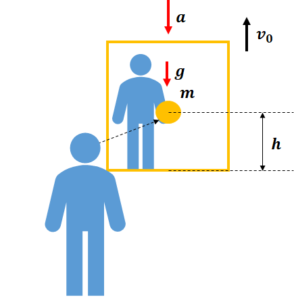
エレベーターとボールの等加速度運動の式をそれぞれ立てていきましょう。
速度が\(v_{0}\)の時のエレベーターの床の位置を\(x=0\)としましょう。
$$エレベーター : x_{elevator}=v_{0}t-\frac{1}{2}at^2$$
$$ボール : x_{ball}=h+v_{0}t-\frac{1}{2}gt^2$$
ここから\(x_{elevator}=x_{ball}\)のとき、\(t=t_{0}\)となります。
$$v_{0}t_{0}-\frac{1}{2}at_{0}^2=h-v_{0}t_{0}-\frac{1}{2}gt_{0}^2$$
これを解いて、
$$t_{0}=\sqrt{\frac{2h}{g-a}}$$
となります。
エレベータ内の視点
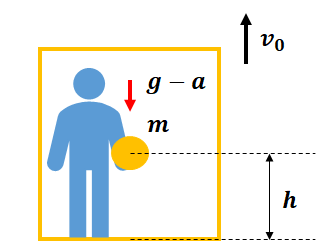
エレベーター内では慣性力が下向きに働きます。
だから見かけの重力加速度\(g’=g-a\)が働きます。
なのでボールについて自由落下運動の重力加速度を\(g’\)として式を立てていきます。
ボールを離すときの位置を\(x=0\)とし、下向きを正にx軸をとります。
$$x=\frac{1}{2}(g-a)t^2$$
\(x=h\)の時に\(t=t_{0}\)なので
$$h=\frac{1}{2}(g-a)t_{0}^2$$
が成り立ち、
$$t_{0}=\sqrt{\frac{2h}{g-a}}$$
となり、両方ともに一致しました。
まとめ
今回は慣性の法則と慣性力の完成について説明しました。
この記事で書いたことは必ず何も見ずに説明できるようにして下さい。
音読したり、自分でまとめたりして、必ず理解し使えるようにしてください。
人に説明できるようになればかなり理解してるといってもいいのでそこを目指してください。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<