仕事で注意するべきポイントと仕事率についてわかりやすく解説します

こんにちは、ほーたです。

今回は仕事と仕事率について解説していきます。

ここの定義をしっかり理解していないと、試験で計算ミスをしたり、物理学習に支障が出てしまうので、しっかり理解してください。

それでは解説していきます。

仕事

仕事とは

物理での仕事とは、物体に力を加えて動かすことを言います。

よく教科書とかでは「（仕事）＝（力）×（移動距離）」で説明しているかもしれませんが、これでは仕事のうち、ほんの一部しか網羅できないので、この記事では一つの式で理解できるように説明していきます。

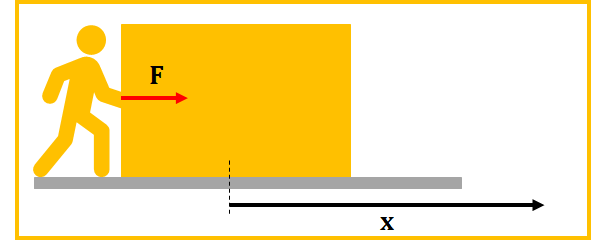
仕事は、

（仕事）＝（移動方向に加えた力\(F\)）×（その力によって移動した距離\(x\)）

と考えてください。これは例があったほうが分かりやすいですね。

これの意味としては、例えば、図のように力が働く場合、移動方向に働く力は\(F_{x}\)なので、移動距離が\(x\)のときの、仕事は、

$$W=F_{x}x$$

と表します。

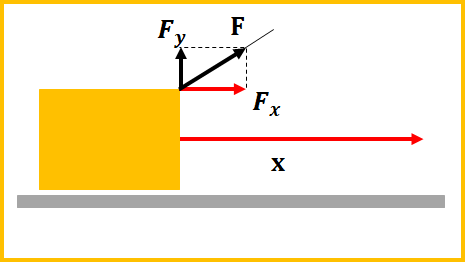
移動方向と垂直の力\(F_{y}\)によって、物体は動いてないので、\(F_{y}\)は仕事をしていない、ということになります。

仕事が\(F\times x\)と表されるのは、一定の力\(F\)で距離\(x\)動かしたときに、そのように表す、ということです。

仕事の単位は[J]（ジュール）で[J]=[N・m]で表されます。

仕事の公式と意識するべきポイント

仕事を扱う上で必ず理解してほしいことが４点あります。

1. 正の向きを決める
2. 力の向きと、物体が動く向きが、逆向きの場合
3. 移動方向と力の向きが直角の場合は、仕事をしていない
4. 力が一定でない場合はグラフから考える

それぞれの場合を、説明していきます。

正の向きを決める

正の向きを決めます。

これは一番大事です。

これをするかどうかで、計算の精度が変わります。

x軸とy軸の向きを決めましょう。

力の向きと、物体が動く向きが、逆向きの場合

これは例えば、図のようになります。

今回は、x軸の向きは右向きなので、正の向きは右向きです。

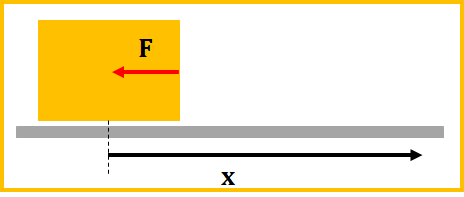
左向きに力\(F\)を加え、右向きに距離\(x\)動くときです。

この時、左向きに力を加えるので、加えた力は\(-F\)、物体は右向きに移動してるので、移動距離は\(x\)になります。

この時の仕事\(W\)は

$$W=(-F)\times x$$

と表されます。

これは、例えば、摩擦によってされた仕事です。

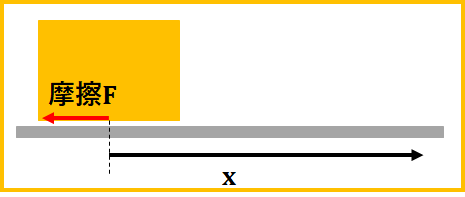
図のように粗い面に物体を滑らせたときに、摩擦が\(-F\)、移動距離が\(x\)の時など、このように計算します。

移動方向と力の向きが直角の場合、仕事をしない

上記で（仕事）＝（移動方向に加えた力）×（移動距離）といったように、移動距離と直角に働く力の場合は、移動方向に加えた力がゼロなので仕事はしません。

だから次の図のように、力\(F\)を、物体が移動する向きと角度\(\theta\)をなすときの仕事を求めるとします。（移動距離は\(x\)とします。）

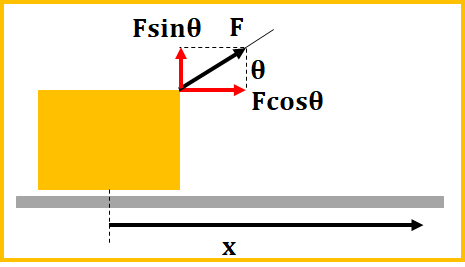
この時、移動方向に加えた力は\(F\cos\theta\)なので、仕事\(W\)は

$$W=F\cos\theta\times x$$

となります。

ミスらない様に気を付けてください。

力が一定でない場合

次に力が一定でない場合です。

物体の位置によって、加える力が変わる場合は、図のような\(F-x\)グラフの面積が、仕事になります。

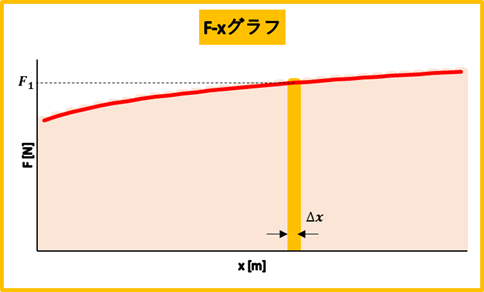
これは、移動距離を微小距離に分けて、その微小距離だけ動かしたときの仕事が、

（仕事）＝（移動方向に加えた力）×（その力によって移動した微小距離）

となり、それらの総和から仕事\(W\)になる、ということです。

例えば、力\(F_{1}\)で距離\(\Delta x_{1}\)だけ動かしたときの仕事\(F_{1}\times\Delta x_{1}\)が、図のオレンジの長方形の面積になる、ということです。

そのように求めた長方形の面積の和が、図の\(F\)-\(x\)グラフの面積になります。

つまり、変化する力の仕事はグラフから求めることが大切になります。

例えば、ばねによる仕事を考えてみましょう。

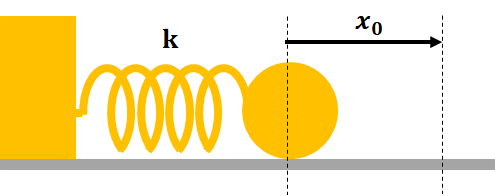
ばねが\(x_{0}\)だけ縮んでる状態で、質量\(m\)の物体を離します。

そして、通常の長さに戻るまでの仕事\(W\)を求めてみます。

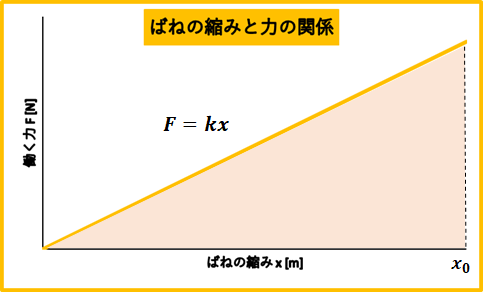
図の面積を求めればいいということになります。

$$W=\frac{1}{2}kx^2$$

それでは仕事について整理しましょう。

3点のポイントにまとめます。

する仕事とされる仕事

図のように、力\(F\)で物体を押し、\(x\)だけ移動させたとします。

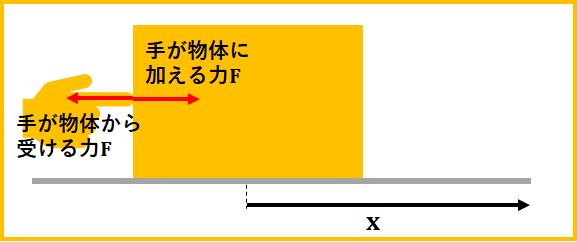
この時、右向きを正の向きとすると、物体は手から力\(F\)を受け、\(x\)だけ移動します。

つまり、手が物体にした仕事\(W_{do}\)は

$$W_{do}=F\times x$$

となります。それに対して、手は物体から力\(-F\)を受け、\(x\)だけ移動します。

つまり、手が物体からされた仕事\(W_{done}\)は

$$W_{done}=(-F)\times x$$

となります。

これから、手がする仕事\(W_{do}\)とされる仕事\(W_{done}\)の関係は、

$$W_{do}=-W_{done}$$

となります。

仕事率

仕事率とは

短時間で大きな仕事が出来るほど、仕事の能率が大きいと言えそうです。

そこで、一秒あたりにする仕事を仕事率\(P\) [W]（W（ワット）=J/s）といいます。

仕事率の公式

仕事率の公式は、定義通り、次のようになります。

一秒あたりにする仕事なので、

（仕事率）＝（移動方向に加えた力）×（一秒間に移動した距離（速度））

となります。

一秒間、一定の力を加えたとすると、式で表すと、

$$P=F\times v$$

となります。

ここで注意してほしいのは、\(t\)秒間にした仕事を\(t\)で割るではありません。

毎秒で同じだけ仕事をしていれば、これが成り立つのですが、仕事が時間によって変わる場合、これは使えないので、要注意です。

まとめ

仕事は\(F\times x\)で覚えがちですが、これでは解けない問題出るので、絶対に今回の記事で書いたような方法で計算するようにしてください。

これが出来るようになれば、計算ミスも減り、仕事を扱う問題でも、かなり解けるようになるので、しっかり理解するようにして下さい。

オリジナルテキストを無料でプレゼントします

僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。

しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。

その一番のきっかけになったのを力学の考え方にまとめました。

力学の基本中の基本です。

色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。

無料配布中です。

もしくは、下記画像をクリック！