こんにちは、ほーたです。
自由落下運動に続き、今度は投げ上げる場合にどのような運動をするのかについて解説していこうと思います。
考え方は自由落下と大して変わりません。
等加速度運動の考え方に従って考えれば、これは暗記ゲーではなく、
イージーになるでしょう。
等加速度運動の考え方や自由落下運動が分からない人は、前回の記事を読んでからこちらを読むことをお勧めします。
【合わせて読みたい】
等加速度運動の考え方
自由落下
鉛直投げ上げ運動の公式を等加速度運動の式から導けるようにする。
目次
鉛直投げ上げを考える上でのポイント
鉛直投げ上げ運動を考えるうえでのポイントは、自由落下運動と同様に鉛直投げ上げ運動は等加速度運動だということです。
つまり、
軸を決定して、初期位置、初速度、加速度を整理し、それを以下の公式に当てはめることが大切になります。
速度 : \(v=v_{0}+at\)
位置 : \(x=x_{0}+v_{0}t+\frac{1}{2}at^2\)
鉛直投げ上げの公式
鉛直投げ上げとは
物体を鉛直上方向に投げ上げたときの運動を鉛直投げ上げ運動といいます。
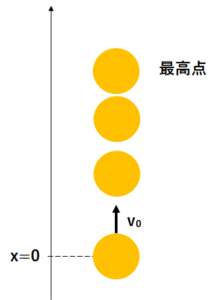
初速度\(v_{0}\)で上に投げて最高点で止まり、そのあと落下し、
発射した点を\(-v_{0}\)で通りすぎる、という運動をします。
つまり運動に対称性があるということです。
けっこう大事な性質。
覚えておきましょう。
鉛直投げ上げの速度の公式
鉛直投げ上げの公式は、
等加速度運動の公式において初速度と加速度がそれぞれ\(v_{0}\)、\(a=-g\)なので、
これを代入すると導けます。
このとき重力加速度はx軸の負の方向に働いているので、負の加速度を持つことになります。
$$v=v_{0}-gt$$
これが鉛直投げ上げの速度の公式です。
鉛直投げ上げの位置の公式
続ては位置の公式を考えていきましょう。
これは等加速度運動の公式において初期位置、初速度と加速度がそれぞれ\(x_{0}=0\)、\(v_{0}\)、\(a=-g\)なので、
等加速度運動の公式に代入すると
$$x=v_{0}t-\frac{1}{2}gt^2$$
となります。
これが鉛直投げ上げ運動の位置の公式。
かならず導けるようにしておきましょう!
速度 : \(v=v_{0}-gt\)
位置 : \(x=v_{0}t-\frac{1}{2}gt^2\)
鉛直投げ下げについて
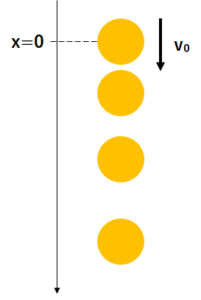
鉛直投げ下げの問題は自由落下の時に、
下向きの初速度を加えたときと同じと考えます。
スタートの位置を原点とし、下向きにx軸をとります。
そうすると初期位置0、初速度\(v_{0}\)、加速度gになるので、自由落下において初速度\(v_{0}\)がつけ足されるだけなので公式は次のようになります。
速度 : \(v=v_{0}+gt\)
位置 : \(x=v_{0}t+\frac{1}{2}gt^2\)
これが鉛直投げ下げについての公式。
自由落下と鉛直投げ上げの応用問題
それではすこし演習をしましょう。
5分くらい考えて分からなければ、答えを見てください。
スピード感をもって読み進めてほしい。
自由落下と鉛直投げ上げの融合問題です。
【問題】
時刻0で地点Aから小球Pを初速度\(v_{0}\)で投げ上げると同時に、Aの真上で高さ\(h\)にある地点Bから小球Qを自由落下をさせるとする。PとQが衝突が衝突するとして衝突したときの時刻\(t_{0}\)を求めよ。ただし重力加速度は\(g\)を用いよ。
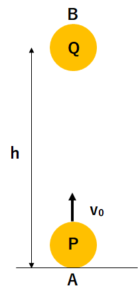
【解答】
まず最初にするべきことは軸を決めることです。
原点と軸の向きを決めます。
基本原点と軸の向きはどこでもいいですが、今回は地点Aを原点として軸の向きは鉛直上向きとします。
そうすると小球Aについて初期位置、初速度、加速度はそれぞれ\(0\)、\(v_{0}\)、\(-g\)、となります。
小球Bについてはそれぞれ初期位置\(h\)、初速度\(0\)、加速度\(-g\)となります。
それでは、
それぞれの小球について等加速度運動の公式に代入していきましょう。
小球Aについて
$$v_{A}=v_{0}-gt$$
$$x_{A}=v_{0}t-\frac{1}{2}gt^2$$
小球Bについて
$$\begin{align}v_{B}=&-gt\\\\x_{B}=&h-\frac{1}{2}gt^2\end{align}$$
さてまずは小球PとQが衝突するのは\(x_{A}=x_{B}\)を満たすので
$$v_{0}t_{0}-\frac{1}{2}gt_{0}^2=h-\frac{1}{2}gt_{0}^2$$
これから
$$t_{0}=\frac{h}{v_{0}}$$
となることが分かりました。【終】
まとめ
このまとめを見て、記事の内容を説明できるまで反復しましょう。
鉛直投げ上げの公式
速度 : \(v=v_{0}-gt\)
位置 : \(x=v_{0}t-\frac{1}{2}gt^2\)
鉛直投げ下げの公式
速度 : \(v=v_{0}+gt\)
位置 : \(x=v_{0}t+\frac{1}{2}gt^2\)
それでは。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<


