力のモーメントとは？？【公式・計算・つり合いをわかりやすく解説】

こんにちは、ほーたです。

めちゃくちゃ大事な単元、剛体の問題、力のモーメント。

これは難しいーって感じる人が多いと思います。

これは僕も高校生の時の物理のテストで初めて60点代を取った分野でした。

当時は「マジかーーーwww」って思ったけど、基礎が分かる今では余裕で簡単な分野です。

この記事を読んで力のモーメントの問題が簡単に解けるように丁寧に解説しているので、

しっかり理解してほしい。

剛体とは

質点と剛体

これは定義通りです。

具体例を出すと、質点は自由落下とか斜方投射とか、

そういう物理現象を考える時に用いた物体のこと。

これによって、大きさがないから回転とか空気抵抗を考えなくてよくなります。

それに対して、

剛体は、大きさがあり変形しない物体なので、

回転を考える必要があります。

これが力のモーメントです。

今からこれを説明しようと思います。

力のモーメントとは

力のモーメントの公式

公式は上記の通り。

ポイントは、力とうでが直角だということです。

これを意識しましょう。

下記図で理解を深めてほしいです。

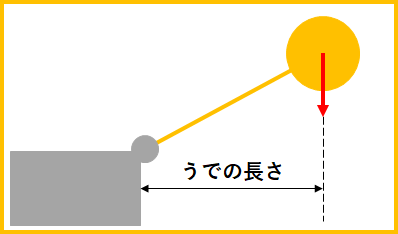
そして、

力のモーメントは、回転を扱う時に使う公式だから、

物体が回転しないときの条件があるはずです。

この条件を力のモーメントのつり合いといいます。

これを立てる時に注意するポイントが3点あるから、それについて説明していきます。

力のモーメントのつり合いの3ステップ

具体的な計算で理解を深めましょう。

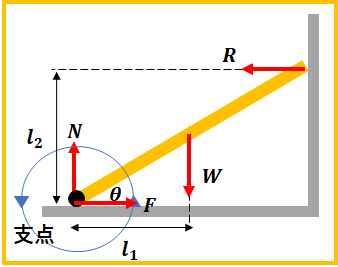
図のように長さ\(2 l\)の棒を壁に立てかける状態を考えます。

粗い面の床からの摩擦を\(F\)、床からの垂直抗力を\(N\)、壁からの垂直抗力を\(R\)、棒にかかる重力を\(W\)、棒の立てかけてる角度を\(\theta\)として、

回転しない条件を考えていきます。

1．視点を決める。

これは未知数が多い点に取ると◎。

今回は図の●

2．正の向きを決める

支点を中心に時計周りの力の正とします。

3．うでの長さを求める。

今回は重力のうでの長さ\(l_{1}\)、壁からの垂直抗力のうでの長さは\(l_{2}\)とします。

$$l_{1}=l cos \theta$$

$$l_{2}=2 l sin \theta$$

4．力の作用線とうでの交点に力を平行移動させて、正負の判断をする。

今回の場合は、重力は時計回りの方向に働いているから負、壁からのい垂直抗力は反時計回りの方向に働いているから正になります。

ここから力のモーメントのつり合いを立てましょう。

$$\begin{align}0=&R \times l_{2}-W \times l_{1}\\\\=&R \times 2 l sin \theta-W \times l cos \theta \end{align}$$

これが回転しない条件。

回転する条件はどうだろうか？？

これを説明していきます。

回転する条件

• 力のモーメントの和が正の時は反時計回りに回転する。
• 力のモーメントの和が負の時は時計周りに回転する。

これ回転条件の問題で使うから、ぜっっっったいに覚えましょう。

うで相撲で有利な人は？？

この力のモーメントを考えて、うで相撲が有利な人について考察する。

うで相撲で勝つには力のモーメントが大きい方が有利になるります。

つまり、同じ力を加えているときは、

うでが短い方が有利になるという事です。

これは相手にかけるモーメントが、自分にかけられるモーメントより大きくなるから。

だから、うで相撲で手首を持った側は有利になるという事ですね。

また、うで相撲で負けたときは、

「俺は弱くない！だって、俺の方がうでが短い！」とか言い訳にしてほしい。

理系同士なら多分盛り上がると思います。多分だけど。(笑)

盛り上がらなくても、これに関しては責任は取らないので自己責任で。

まとめ

このまとめを見て、記事の内容を説明できるまで反復しましょう。

それでは。

オリジナルテキストを無料でプレゼントします

僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。

しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。

その一番のきっかけになったのを力学の考え方にまとめました。

力学の基本中の基本です。

色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。

無料配布中です。

もしくは、下記画像をクリック！