こんにちは、ほーたです。
今回は、超重要な分野
円運動です。
実際に初めて授業で説明を受けたときは、
あれ?ついていけない...
って人も多いと思います。
これは入試に頻出ですし、
これが理解出来なければ、
大問ほとんど解けないという悲惨な事態にもなりうるので、
必ず理解するようにして下さい。
向心加速度と遠心力を深く理解し、等速円運動を根っこから説明できるようにする。
目次
円運動とは
等速円運動・・・向心力が働くことで一定の速度で円軌道を描く運動のこと
円運動って
なんで円軌道になるかを考えたことがありますか??
公式だけ覚えて、
適当に応用するでは、
のちに通用しなくなります。
向心加速度を理解すれば、
これが解決します。
等速円運動と向心加速度
ここでは、
- 向心加速度が働く→等速円運動をする
- 等速円運動をする→向心加速度が働く
という事を説明していきます。
「A→BかつB→AならばA⇄B」パターンです。
向心加速度が働く→等速円運動をする
物体が進む向きに対して、
垂直に力が働くとどのような運動になると思いますか??
少し考えてみて下さい。
一定の力であれば、下の図のように3種類に分かれるでしょう。
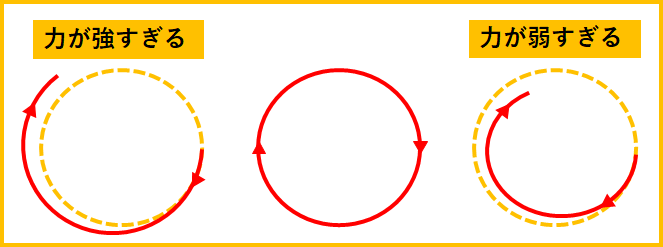
力が強いと内側へ、
力が弱いと外側へ、
そしてちょうどいい力が働くときに円運動をする事になります。
そして進行方向と垂直の向きに力が働いているので、
これは円の中心方向に向いている力という事になります。
中心に向かって力が働いているという事は、
中心方向に加速しているという事になります。
この特殊な加速度を向心加速度といいます。
また、この時の力を向心力といいます。
よって、1番の「向心加速度が働く→等速円運動をする」は分かりましたね。
(実際の証明はもっと難しいです。
これは大学で勉強してください。)
等速円運動をする→向心加速度が働く
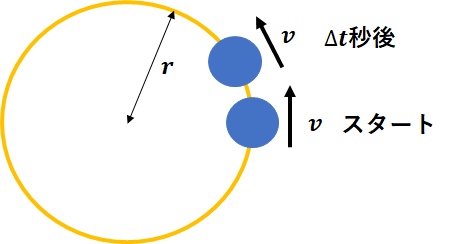
ここは少しややこしいです。
図のように等速円運動をしてる物体を考えます。
初期位置からだけ\(\Delta t\)経過したときの運動の変化について考えましょう。
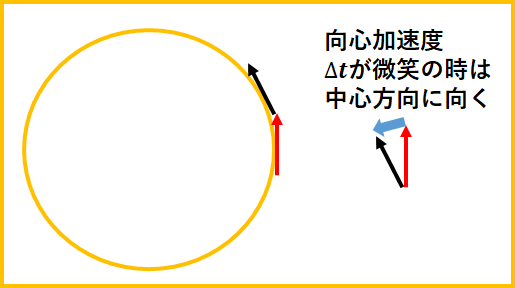
この時に移動した分だけ速度の向きは変わります。
この時に速度の変化の方向が中心向きになるから、
力が中心方向に働いているという事になります。
これが向心力で加速度が向心加速度です。
ここも詳しい証明は大学で勉強してください。
捕捉1
以上から向心加速度⇄等速円運動という事が分かったのですが、
ここでかなり重要な考え方の復習が出来るので、
それについて解説していきます。
向心力は物体の進行方向と垂直の向きに働くので、
向心力は物体に対して仕事は一切していない、
という事になります。
だから物体の速度は一定になります。
進行方向と力が垂直の時、
その力は物体に対して仕事をしていない。
これはマジで大切なので、
必ず理解しておきたいところです。
捕捉2
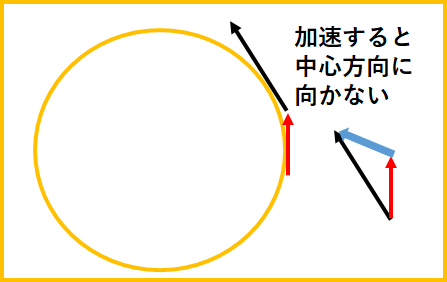
等速でない場合は、
中心に向かって力あが働かなきません。
下の図のようなイメージです。
円運動の公式
速度 : \(v=r\times\omega\)
向心加速度 : \(a=v\times\omega=r\times\omega^2=\displaystyle\frac{v^2}{r}\)
向心力 : \(m\times a\)
大きくはこの2つの公式が大切になります。
角速度
角速度についてはこちらの記事を読んで下さい。
かなり詳しく書いていますし、
超重要な公式の解説もしています。
向心加速度
向心加速度の公式を証明していきましょう。
今回は、この図から証明してきます。
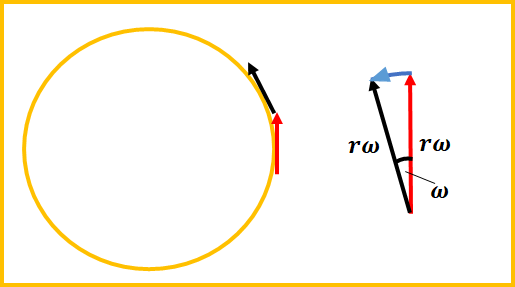
$$a=r\times\omega^2$$
が分かります。
さらに\(v=r\times\omega\)から
$$\begin{align}a=&r\times\omega^2\\\\=&\frac{v^2}{r}\\\\=&v\times\omega\end{align}$$
という事が分かります。
公式が分かったところで、
円運動の視点について考えていきます。
向心力と遠心力についてです。
遠心力とは
遠心力・・・観測者が物体と同じく回っているときに見える力(円運動の慣性力)
公式 : \(F=ma=mv\omega=mr\omega^2=\displaystyle\frac{v^2}{r}\)
慣性力については、こちらに書いています。
これだけではイメージしずらいと思うので、
円形サーキットを回る車でイメージしましょう。
- 大地から見た時
- 車に乗っている時
で解説していきます。
大地から見た時
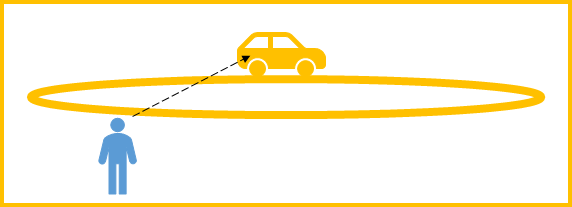
大地から見たときは、
図のような力の作図になります。
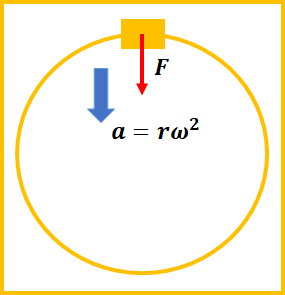
中心方向に向心加速度が働いているので、
運動方程式は次のようになります。
$$mr\omega^2=F$$
車に乗っている時

車に乗っていると、
車は円運動をしてるように見えません。
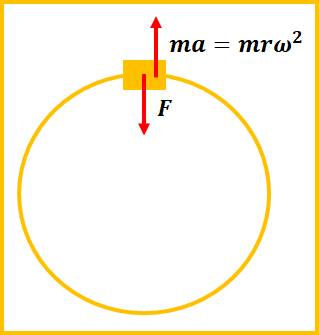
図のような力の作図になり、
車の運動方程式は、
$$0=F-mr\omega^2$$
になります。
この時の\(mr\omega^2\)を遠心力といいます。
カーブを曲がるときに外側に引っ張られる感じがするのは、
遠心力が働くからです。
このように視点によって、
働く力が変わります。
まとめ
このまとめを見て、記事の内容を説明できるまで反復しましょう。
【等速円運動】
・・・一定の速度で円軌道を描く運動。この時向心力が働いている
【等速円運動の公式】
角速度\(\omega\)
速度 : \(v=r\omega\)
周期 : \(T=\displaystyle\frac{2\pi}{\omega}\)
回転数 : \(n=\displaystyle\frac{1}{T}\)
向心加速度\(a\)
\(a=v\omega\)
向心力
\(mr\omega^2\)
【遠心力】
・・・回転してる人が見える力
遠心力の公式 \(mr\omega^2\)
それでは。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<


