運動方程式からわかること

運動方程式と聞いて何がパッと浮かびますか？

\(ma=F\)でしょうか？？

それと、

• 質量が大きいと加速しにくくなる
• 力が小さいと加速しにくくなる

でいいでしょうか？

そのうち二つの

• 質量が大きいと加速しにくくなる
• 力が小さいと加速しにくくなる

は運動方程式から読み取れることなのですが、

そもそも

\(ma=F\)という理解の仕方は間違っています。

これには、

なんで？と思う人も多いでしょう。

運動方程式は正確には

$$m\vec{a}=\vec{F}$$

です。ここからわかるように加速度と力はベクトル量なんです。

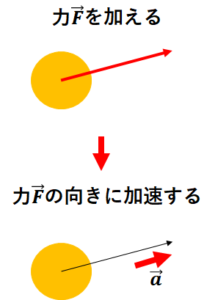
つまり、物体は加えた力の方向に加速するという事です。

この記事では運動方程式がベクトル量であることを用いて、普段運動方程式を立てるときにxとy成分でに分ける理由を示していこうと思います。

ベクトル量\(\vec{A}=\vec{B}\)とは、\(\vec{A}\)と\(\vec{B}\)が「大きさが等しく、さらにその向きが等しい」という事を言っています。だから異なる向きのベクトルが等しくなることはまずありません。（当たり前ですね。）

これを踏まえて運動方程式について考えましょう。

まず物体に力\(\vec{F}\)を加えます。そうすると物体はその力\(\vec{F}\)の向きに加速度\(\displaystyle\frac{\vec{F}}{m}\)で進みます。

次に複数の力\(\vec{F_{1}}\)、\(\vec{F_{2}}\)、\(\vec{F_{3}}\)を加えるとどうなるでしょうか？

まず最初にするべきは、3つの力を足します。

$$\vec{F}=\vec{F_{1}}+\vec{F_{2}}+\vec{F_{3}}$$

とします。この\(\vec{F}\)を図で表してみます。まず、それぞれの力の作用線を描きます(1)。そして、それぞれの力を作用線上に動かしてベクトルの始点を合わせます(2)。そして、ベクトルの和を図に示します(3)。

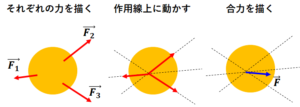
力\(\vec{F}\)を図示出来たら運動方程式を立てましょう。

$$m\vec{a}=\vec{F_{1}}+\vec{F_{2}}+\vec{F_{3}}=\vec{F}$$

つまり、物体は\(\vec{F}\)の向きに加速するという事になります。

ここで注目すべきは物体は力\(\vec{F_{1}}\)、\(\vec{F_{2}}\)、\(\vec{F_{3}}\)の向きに加速するのではなく、その合力の向きに加速します。

それでは例を考えてみましょう。

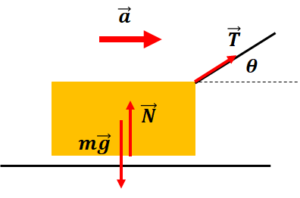
この時に運動方程式を立てると、

$$m\vec{a}=\vec{T}+m\vec{g}+\vec{N}$$

になります。ここで、ベクトルの概念を考えます。

$$\begin{eqnarray*}& &\vec{T}=(T\cos\theta,T\sin\theta)\\\\& &\vec{a}=(a,0)\\\\& &\vec{N}=(0,N)\\\\& &g=(0,-g)\end{eqnarray*}$$

とすると、

$$m(a,0)=(T\cos\theta,T\sin\theta)+m(0,-g)+(0,N)$$

となるので、結果的にxとy成分で考えることが出来ます。

$$\begin{eqnarray*}& &x \ : \ ma=T\sin\theta\\\\& &y \ : \ 0=T\sin-mg+N\end{eqnarray*}$$

以上から運動方程式をx、y成分に分けて考えることは運動方程式が

$$m\vec{a}=\vec{F}$$

だからということになります。

というわけで、運動方程式は単に\(ma=F\)で理解するのではなく、ベクトル量として理解するようにしましょう。

このまとめを見て、記事の内容を説明できるまで反復しましょう。

それでは。

オリジナルテキストを無料でプレゼントします

僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。

しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。

その一番のきっかけになったのを力学の考え方にまとめました。

力学の基本中の基本です。

色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。

無料配布中です。

もしくは、下記画像をクリック！