角速度とは？？【公式・単位などをわかりやすく解説】

力学

力学

こんにちは、ほーたです。

角速度。

円運動や単振動をする上で理解必須です。

ここを理解できなければ、

円運動を扱うのはかなり難しくなりますし、

円運動の現象を解析するのにかなり不利になります。

確実に理解していきましょう！

この記事で身につくこと

角速度を深く理解し、角速度から連想できる公式を整理する。
また、円運動を勉強する土台をつける。

角速度とは【定義・単位】

角速度とは

角速度$\omega$・・・1秒間あたりの回転角（ラジアン）
単位 : [rad/s]

具体的にどのようなことを言っているかを解説していきます。

あなたがハンマー投げしてるシーンを思い浮かべてください。

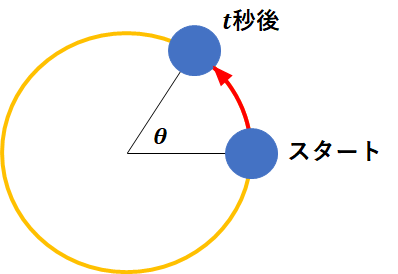
円の中心であなたが回転しており、

おもりが一定の速度で回転してるとします。

そして、おもりが$t$秒後に角度$\theta$[rad]だけ回転した時の角速度$\omega$[rad/s]は、

$$\omega=\frac{\theta}{t}$$

という事になります。

1秒で$\omega$だけ回転するという事です。

角速度の公式

角速度の公式

角速度$\omega$[rad/s]と速度$v$[m/s]、円の半径$r$[m]との関係
$v=r\times\omega$
角速度$\omega$[rad/s]と周期$T$[s]の関係式
$T=\displaystyle\frac{2\pi}{\omega}$
角速度$\omega$[rad/s]と回転数$n$[回転/s]の関係
$n=\displaystyle\frac{1}{T}=\displaystyle\frac{\omega}{2\pi}$

これだけではわかりにくいという人もいると思うので、

順番に詳しく解説していきます。

上のハンマー投げの例で説明していきます。

これを理解する上で、

弧度法について理解してる方がいいので、

先に下記の記事を読んで下さい。

→弧度法と度数法の違いは？？【公式・単位などをわかりやすく解説】

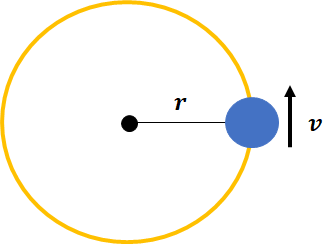
角速度と速度、円の半径との関係

弧長の公式$l=r\times\theta$から求めていきましょう。

一定の角速度$\omega$で運動している時、

$\Delta t$秒間で$\Delta\theta$[rad]だけ移動したとすると、

$$\Delta\theta=\omega\times\Delta t$$

となり、一定の速度$v$で移動する時、

$\Delta t$秒間で$l$だけ移動したとすると、

$$l=v\times\Delta t$$

となります。

これを弧長の公式に代入します。

$$\begin{align}v\times\Delta t=&r\times\omega\times\Delta t\\\\\Leftrightarrow \ v=&r\times\omega\end{align}$$

これで公式が求められました。

角速度と周期の関係

まず周期とは、円運動が1周回るのにかかる時間のことです。

つまり、

スタート地点から1周してまた同じ場所に戻った時の時間という事ですね。

その周期と角速度の関係を求めていきます。

角速度$\omega$[rad/s]で運動している物体が、

1周（$2\pi$[rad]）するのにかかる時間が周期$T$[s]。

$$\begin{align}\omega\times T=&2\pi\\\\\Leftrightarrow \ T=&\frac{2\pi}{\omega}\end{align}$$

これで周期と角速度の関係が導けました。

角速度と回転数の関係

回転数$n$[回転/s]とは、1秒間に何回転するかのことです。

波動の分野では振動数といいますね。

周期は$T$秒間で1回転するという意味なので、

1秒経つ内に$T$が何個入っているか、

というイメージです。

つまり、1秒を$T$秒で割るればいいという事です。

$$\begin{align}n=&\frac{1}{T}\\\\=&\frac{2\pi}{\omega}\end{align}$$

まとめ

このまとめを見て、記事の内容を説明できるまで反復しましょう。

この記事のまとめ

角速度$\omega$[rad/s]・・・1秒間あたりの回転角[rad]

角速度の公式
角速度$\omega$[rad/s]と円の半径$r$[m]、速度$v$[m/s]の関係式
$v=r\times\omega$
角速度$\omega$[rad/s]と周期$T$[s]の関係
$T=\displaystyle\frac{2\pi}{\omega}$
角速度$\omega$[rad/s]と回転数$n$[回転/s]の関係式
$n=\displaystyle\frac{1}{T}=\displaystyle\frac{\omega}{2\pi}$

それでは。