こんにちは、ほーたです。
今回は垂直抗力と摩擦力について。
ここでミスると全てミスります。
これは入試でほぼ確実に出る大事な分野なので、しっかり読み込んでいきましょう。
垂直抗力を理解するとともに3種類の摩擦力の使い方をマスターする。
目次
垂直抗力
垂直抗力とは
垂直抗力とは、物体が接触しているほかの物体の面から垂直方向に受ける力にことをいいます。
例えば、図のような体系を考えてみましょう。
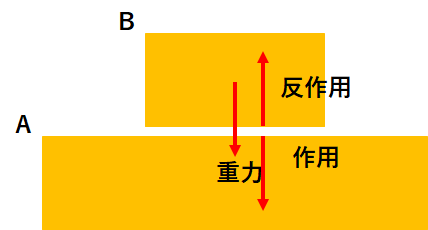
物体Bが物体Aを押すと、当然物体Aは物体Bから力を受けます。
そして、その反作用として物体Bは物体Aから力を受けます。
これが垂直抗力です。
垂直抗力は重力の反作用ではないことに要注意。
これマジで間違いガチだから、しっかり覚えてください。
ではどうやって垂直抗力を求めるのか??
垂直抗力の求め方
垂直抗力を求めるにあたってのポイントは力の作図。
力の作図については下記の記事に書いているので、詳しくはこちらを読んでください。
垂直抗力は接触してる物体の接触面の垂直方向に受ける力なのでポイントとしては、
以下の4点。
- xとy軸の向きを決める(正の方向)
- 力の作図。
- 運動方程式または力のつり合いを立てる。
- 方程式を解く。
マジで大切なのでこれ通りに求めて下さい。
これではなかなかイメージができないと思うので具体例を考えてみましょう。
物体Aの上に質量\(M\)の物体Bを乗せたとき。
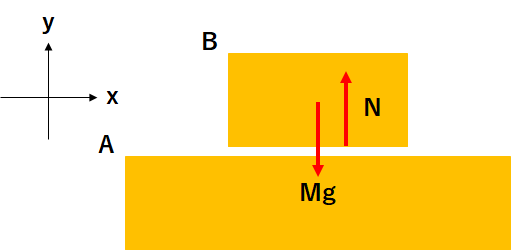
1.xとy軸の向きを決める。
x軸を水平方向、y軸を垂直方向にとる(上図)。
2.力の作図(上図)。
3.力のつり合い、運動方程式
$$y:0=N-Mg$$
4.方程式を解く
上の方程式を解くと
$$N=Mg$$
となります。
この手順で垂直抗力は求まります。
セオリー通り解けば、しかっり求まるのでこれを意識することが大切です。
摩擦力
摩擦力は接触面が粗いと働く力です。
問題文に粗いと書いていれば摩擦が働きます。
なめらかと書いていれば摩擦は働きません。
そして摩擦力の向きは物体の進行方向を妨げる方向に働きます。
つまり前に進む物体には後ろに働くということです。
これを頭に入れて摩擦力について勉強していきます。
3つのタイプの摩擦力
何かを引っ張ったり、押したりするとき次のような経験があると思います??
「最初はなかなか動かないけど、力を強くしていくとあるときにカクっと物体が軽くなるように感じ、それ以降簡単に動かせる」
このようなに粗い面上の物体を動かそうとするときには、実は次の三段階で摩擦力が働いています。
物体を引っ張る(押す)ときまずは静止摩擦力が働き(1)、引っ張る(押す)力を強くすると最大静止摩擦力に達する(2)。そうなるとカクっと物体が軽くなったような感じがし動き始める(3)、という流れで摩擦力のタイプが遷移します。

『物体がびくともしない(1)→物体が滑る直前(2)→物体が滑る(3)』
という感じです。
滑る直前とは、滑り出した、滑り始めたも入ることは要注意。
それではそれぞれの段階の摩擦力について説明していきます。
静止摩擦力
まずは静止摩擦力について。
静止摩擦力とは物体が静止してるときに働く摩擦力をいいます。
この静止摩擦力は物体がびくともしないときに働く力で、加わる力に応じて変化します。
これはどんなに力を加えても物体が動かないときに働いている摩擦力です。
加える力によって摩擦力が変わり、静止摩擦力は未知数の値\(F\)をとります。
$$静止摩擦力:F$$
さらに物体が動き出す瞬間の摩擦力を最大静止摩擦力と呼びます。
そして最大静止摩擦力は垂直抗力に比例しており、この比例定数\(\mu\)を静止摩擦係数と呼びます。
$$最大静止摩擦力:\mu N$$
動摩擦力
次に動摩擦力について。
動摩擦力とは物体が動いてるときに働く摩擦力をいいます。
この動摩擦力は垂直抗力に比例しており、この比例定数\(\mu’\)を動摩擦係数といいます。
$$動摩擦係数:\mu’ N$$
この動摩擦力は物体が滑る速さによらず一定の値をとります。
また\(\mu'<\mu\)なので動摩擦係数は静止摩擦係数よりも小さい値をとります。
だから物体が動き出したら、動かすのが楽になります。
摩擦を扱う問題を解くときに大切にしてほしいのは、「今どの段階を扱うべきか」を常に意識することです。
それでは三種類の摩擦力をまとめます。
1.びくともしない : 静止摩擦力 : \(F\)
2.滑る直前 : 最大静止摩擦力 : \(\mu N\)
3.もう滑っている : 動摩擦力 : \(\mu’ N\)
垂直抗力と摩擦力の問題
それでは練習問題を解いて理解を深めましょう。
【問題】
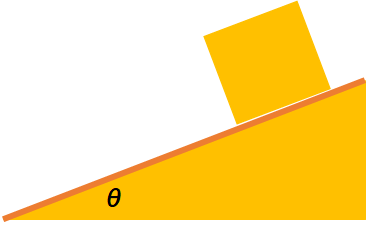
図のような体系で質量\(M\)の物体と斜面の動摩擦係数を\(\mu’\)とする。そして\(\theta=\theta_{0}\)の時物体が滑りだしたとする。この時\(\theta<\theta_{0}\)、\(\theta=\theta_{0}\)、\(\theta>\theta_{0}\)の場合での摩擦力を求めよ。また最大静止摩擦係数を求めよ。
【解答】
上記の垂直抗力の求め方に沿って垂直抗力を求める。➀xとy軸の向きを決める(下図)➁力の作図(下図)③運動方程式または力のつり合い④それを解く、これを徹底していきます。
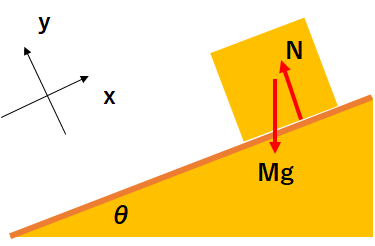
③のy軸の力のつり合いを考えます。
$$0=N-mg\cos\theta$$
よって垂直抗力は
$$N=ma\cos\theta$$
となります。\(\theta\)の値で場合分けします。
1). \(\theta\leq\theta_{0}\)の時
③のx軸の力のつり合いを考えます。
$$\begin{align}&0=f-mg\sin\theta\\\\&\Leftrightarrow f=mg\sin\theta\end{align}$$
\(\theta<\theta_{0}\)の時は静止摩擦力が働き、\(\theta=\theta_{0}\)の時は最大摩擦力が働きます。このとき、
$$\begin{align}f=&mg\sin\theta_{0}\\\\=&\mu mg\cos\theta_{0}\end{align}$$
これから最大静止摩擦係数は
$$\mu=\tan\theta_{0}$$
2). \(\theta>\theta_{0}\)の時
\(\theta>\theta_{0}\)の時は物体が斜面上を滑り始めます。
なので動摩擦力が働きます。
$$f=\mu’ ms\cos\theta$$
となります。【終】
まとめ
このまとめを見て、記事の内容を説明できるまで反復しましょう。
垂直抗力の求め方
1.正の方向を決める
2.力の作図
3.運動方程式または力の作図
4.方程式を解く
3種類の摩擦力
1.静止摩擦力 : \(F\)
2.最大静止摩擦力 : \(\mu N\)
3.動摩擦力 : \(\mu’ N\)
それでは。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<