こんにちは、ほーたです。
今回は水圧とアルキメデスの原理(浮力)について解説していきます。
浮力は公式だけ覚えてあまり公式の証明や水圧について考察したことがある人が少ないと思うので、水圧の理解も深まるようにわかりやすく説明していきます。
水圧の原理をより深く理解し、それに基づいて浮力の公式を証明できるようになる。
目次
水圧の考え方
水圧とは??その単位は??
水圧とは水が、大気圧とは大気が単位面積(1 m²)あたりに押す力になります。
なので単位はパスカル[Pa](=[N/m²])です。
まずは、大気圧が\(p_{0}\) [N/m²]における、水深\(d\) [m]の場所における水圧\(P\) [N/m²]を求めていきましょう。
ここで、\(\rho_{water}\) [kg/m³]を水の密度とします。
密度とは、単位体積(1 m³)当たりの質量のことでしたね。
水圧の計算
それでは水深\(d\) [m]での水圧を求めていきましょう。
ここでポイントは図のように断面積1 m²を底面に持つ、水面から深さ\(d\) [m]までの水の柱を描くことです。
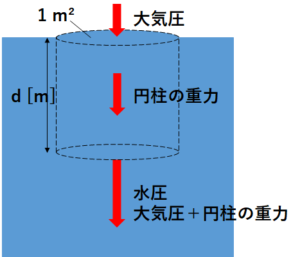
そうすれば水深\(d\) [m]の面が受ける力を求める、という問題に変わります。(底面の面積が1 m²だから)
(ここからは水深\(d\) [m]までの円柱を円柱Aと書きます。)
次のような図を考えてみましょう。
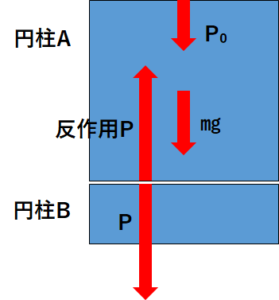
水深\(d\) [m]における水圧\(p\) [N/m²]は、上の図でいうと円柱Bが円柱Aから受ける力\(P\) [N]と等しくなります。
そして問題を解くイメージとして円柱Aが円柱B上に乗っていて、上から力\(P_{0}\) [N]を受けている、という問題と同じになります。
また円柱Aの質量\(m\)は(密度)×(体積)で表され、密度が\(\rho_{water}\)[kg/m³]、体積が\(d[m]\times1[m²]\)なので、質量\(m=\rho\times d\) [kg]となります。
それでは円柱Aについて力のつり合いを立てていきましょう。
円柱Aは円柱Bから力P [N]の反作用を受け手いることに注意です。
$$A : 0=P-P_{0}-mg$$
よって水深\(d\) [m]での水圧は
$$P=P_{0}+\rho_{water} d g$$
となることが分かります。
$$P=P_{0}+\rho_{water}dg$$
同じ水深では水圧は同じになります。
次のパートではこの同じ深さでは水圧が等しいということについて具体的に考察していきます。
圧力のつり合いを考える➀
図のような、面積\(S\)の円形の軽いピストンAと面積\(2 S\)の円形の軽いピストンBがあって内部は密度\(\rho\)の液体で満たされている状態を考えましょう。
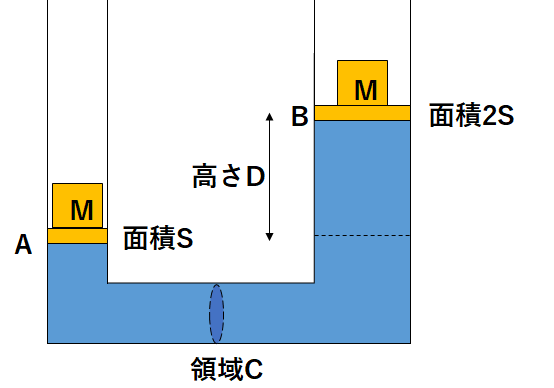
ピストンAとピストンBには質量\(M\)の物体がのっている時のピストンAとピストンBの高さの差\(D\)はいくらになるかを考えていきましょう。
ここで大切なのは深さが同じであれば水圧は同じであるということです。
となると図の領域Cで圧力が一定になる必要がありますよね。
そのためにはピストンAと同じ高さの水圧が左右で等しくなければ、領域Cでの水圧が一定にならないことになります。
つまりここではピストンAの位置で圧力のつり合いを考えるのです。
(ピストンA側での水圧)=(ピストンB側での水圧)
これを考えることが大切です。ここはミスりやすいのでしっかり理解しておいてくださいね。
ピストンB側での水圧は
(質量\(M\)による圧力)+(高さ\(D\)内にある水による圧力)
なので、文字を用いたつり合いの式は
$$\frac{Mg}{S}=\frac{Mg}{2 S}+\frac{\rho\times D\times 2 S\times g}{2 S}$$
となります。
ここから\(D=M/2\rho\)と求まります。
圧力のつり合いを考える➁
次に水面の高さが変わる方法についてとなぜかを解説します。
これでしっかり理解を深めてください。
次のステップで水面を上げることが出来るので試してみて下さい。
- コップに半分くらい水を入れた状態で水に沈める
- コップの口を水面にそろえる(揃えなくても水面の上昇が確認できればいい)
これをするだけで水面が高くなります。
さてなぜでしょうか??
これも同じ深さでは水圧が同じということが関係しています。
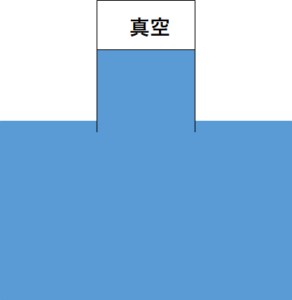
コップの真下の水圧とそれ以外の水圧が等しくなるためには、コップの部分の水面が大気圧と等しくなるまで上がる、というわけです。
(大気圧)=(コップ内の水による圧力)
となるというわけです。
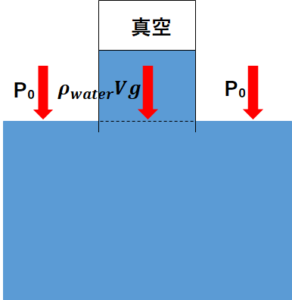
例えば、水面より上に出てる水の体積が\(V\)、コップの口の面積を\(S\)だとすると、大気圧を\(P_{0}\)、水の密度を\(\rho_{water}\)とすると、
$$P_{0}=\frac{\rho_{water}\times V\times g}{S}$$
が成り立つということです。
【捕捉】水の出る勢い
捕捉というか水深によって水圧がかわるということを実感できるようなことがあるので、それについて少しお話ししようと思います。
図のようにペットボトルに穴をあけます。
そうすると穴をあける位置によって水の出る勢いが変わります。
水圧が大きいペットボトルの下の方ほど出る勢いが強くなります。
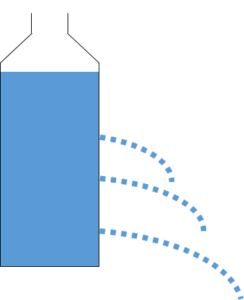
水圧が大きい方が水の出る勢いが強いのはイメージつきますよね。
興味がある方は実際に実験してみるといいですね。
かなり簡単に出来るので。
また、これを面白い!!と思う方は大学で物理を勉強するといいですね。
浮力の考え方
氷はなぜ水に浮くのでしょうか??
ヘリウムガスの入った風船が空中を飛んでいくのはなぜでしょうか??
浮力を理解すれば式的に理解することが出来ます。
浮力とは文字通り「浮かす力」です。
液体中や気体中にある物質は、液体や気体から圧力を受けている。
物質の各面が受ける力をすべて足し合わせると、上向きの力が残ります。
浮力とはこれのことです。
浮力の公式【アルキメデスの原理】
密度\(\rho\) [kg/m³]の液体に体積\(V\) [m³]の物体を沈めた時、物体に働く浮力の大きさ\(F\) [N]は次の通りに表されます。
$$F=\rho Vg$$
浮力の公式の求め方
それでは浮力の公式を求めていきましょう。
図のように底面積\(S\) [m²]、高さ\(H\)の物体を大気圧\(P_{0}\) [N/m²]の元の密度\(\rho_{water}\) [kg/m³]の水に沈めたときの浮力\(F\) [N]を求めていきます。
物体を沈める深さは\(d\) [m]とします。
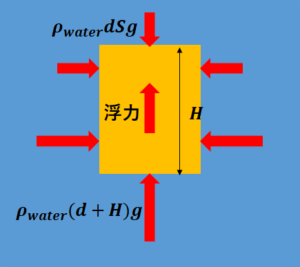
そうすると水圧の公式から物体の上面、下面から働く水圧\(P_{1}\) [N/m²]、\(P_{2}\) [N/m²]は
$$上面 : P_{1}=P_{0}+\rho_{water}dg$$
$$下面 : P_{2}=P_{0}+\rho_{water}(d+H)g$$
となります。
浮力はこの二つの水圧の差によって生まれます。
$$F=(P_{0}+\rho_{water}(d+H)g)\times S-(P_{0}+\rho_{water}dg)\times S$$
ここから浮力\(F\) [N]は
$$F=\rho_{water}Hg\times S$$
となります。
物体の体積\(V\) [m³]は\(V=S\times H\)なので
$$F=\rho_{water}Vg$$
と求まりました。
氷が水に浮く、ヘリウムの入った風船が飛んでいく理由
それでは最初の質問に戻りましょう。
今回は一般的に密度\(\rho_{1}\)の液体に密度\(\rho_{2}\)、体積\(V\)の物体を沈めた場合を考えましょう。

運動方程式を考えます。
$$\begin{eqnarray}ma=&\rho_{1}Vg-\rho_{2}Vg\\\\=&(\rho_{1}-\rho_{2})Vg\end{eqnarray}$$
ここでこの物体が浮く条件は加速度\(a>0\)なので、これを満たすには\(\rho_{1}>\rho_{2}\)、つまり物体の密度が液体の密度よりも小さいということが条件になります。
これが物体が液体より軽いとは密度の比較なのです。
密度が軽い方が浮く。
まとめ
今回のまとめとしては、水圧の原理について二つの例にわたって理解し、さらにそれに基づいて浮力について理解したということになります。
結構難しいことを書いたかもしれませんが、このレベルのことは簡単に考察できないと基礎があるとは言いません。
応用に見えて考える材料はすべて基本的なことなので基礎をつければこれくらいの考察は簡単になります。
分からなければ何度も読んで、それでもだめなら人に行くなどして必ず理解するようにしてください。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<