こんにちは、ほーたです。
今回は運動エネルギーについて説明していきます。
仕事との関係性を用いて公式を導出していくので、仕事についての理解も深まります。
この記事を読む前に、「仕事のポイント」と「する仕事とされる仕事」が重要になるので、それについての理解をしてから、読むことをおススメします。
【合わせて読みたい】
仕事のポイント、する仕事とされる仕事
→仕事で注意するべきポイントと仕事率についてわかりやすく解説します
それでは解説していきます。
運動エネルギーを仕事の考え方から導き、前回の記事の「仕事の考え方」をより深く理解する。
目次
運動エネルギーとは
エネルギー
エネルギーとは相手に仕事をする能力の事を言います。
例えば、図のように、ハンドボールを片手でキャッチしようとすると、手が持っていかれますね。
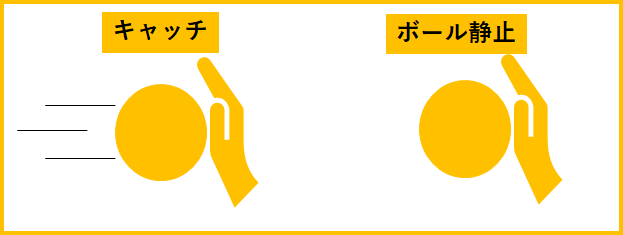
この時ボールはエネルギーを持っている、ということになるのです。
運動エネルギー
野球ボール60キロをキャッチするよりも、ハンドボール60キロを片手でキャッチする方が、手がもっていかれる感じがします。
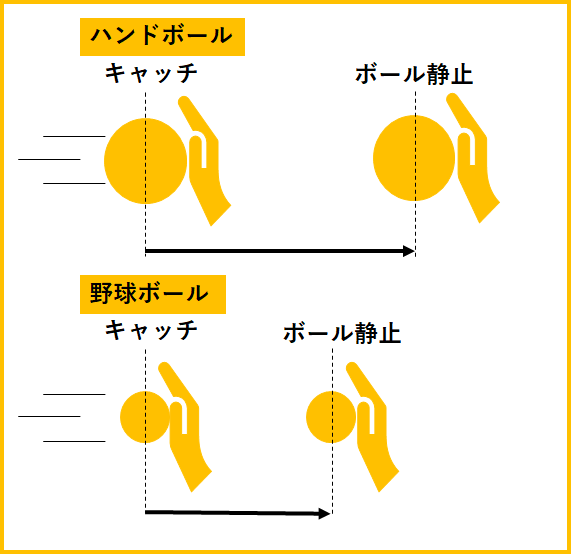
このように、物体は、重ければ重いほど、速ければ速いほど、相手に仕事をする能力がある、つまり、エネルギーがあると言えます。
このような早くて重い物体が持つエネルギーのことを運動エネルギー\(K\)[J]といいます。
運動エネルギーの公式とその求め方
運動エネルギーの公式
運動エネルギーは物体の質量\(m\)に比例し、速さ\(v\)の二乗に比例します。
$$K=\frac{1}{2}mv^2$$
それではこの公式を求めていきます。
運動エネルギーの公式の求め方
図のように、質量\(m\)、速さ\(v\)の弾丸が粘度に打ち込まれる状況を考えましょう。
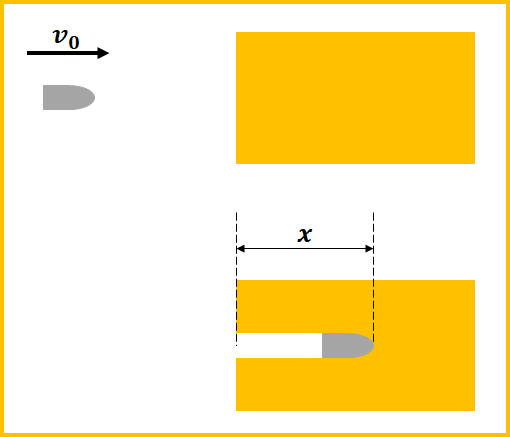
この弾丸が常に力\(F\)を受けながら減速すると仮定し、粘度の中を\(x\)だけ移動して止まった時に、弾丸が粘度にする仕事\(W_{do}\)を考えていきます。
この時求める運動エネルギー\(K\)は、弾丸が粘度にする仕事\(W_{do}\)に等しいですね。
$$K=W_{do}$$
しかし、粘度が弾丸にする仕事を求めるのは難しいので、弾丸が粘度にされる仕事\(W_{done}\)を求めて、「する仕事とされる仕事の関係\(W_{do}=-W_{done}\)」から運動エネルギーを求める、という導出方法で行きます。
それでは、仕事の考え方から考えていきます。
- 正の向きを決める
- 力が変化する場合はグラフから求める。
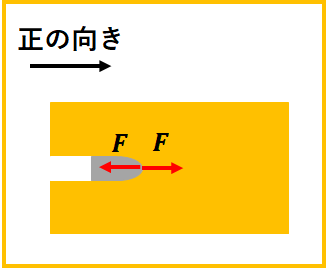
正の向きは、右向きにとり、力は一定なので、(移動方向に加える力×移動距離)から弾丸が粘度にされた仕事\(W_{done}\)を求めましょう。
弾丸が粘度から受ける力は\(-F\)、弾丸の移動距離は\(x\)なので、弾丸が粘度にされる仕事は
$$W_{done}=(-F)\times x$$
となります。
弾丸についての運動方程式は
$$ma=-F$$
なので、
$$W_{done}=ma\times x$$
が得られる。そして、等加速度運動の公式
$$0^2-v^2=2a(x-0)$$
より、
$$W_{done}=m(\frac{-v^2}{2x})=-\frac{1}{2}mv^2$$
となります。よって、運動エネルギー\(K\)は、\(K=W_{do}=-W_{done}\)より、
$$K=\frac{1}{2}mv^2$$
と導けれます。
実際に具体的な計算をしてみよう
問題
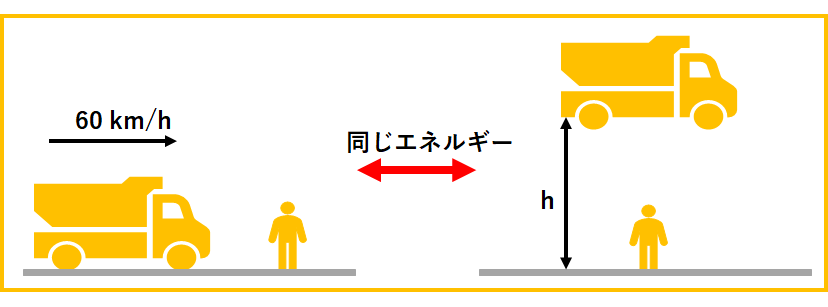
重さ1トン(1000 ㎏)のトラックが60 km/hで走っているときの運動エネルギー\(K\)[J]を求めよ。また、これはトラックをどれくらいの高さから落としたときのエネルギーに相当するか。その高さ\(h\)[m]も求めよ。
解答
まず60 km/hは1時間で60キロ走るので、単位をm/sに直すと、
\(60\) km/h\(=16.6…\) m/s
になります。よって運動エネルギーは
\(K=\frac{1}{2}\times 1000\times (16.666…)^2=139445\) J
となります。
(今回は有効数字を考えず求めました)
次に、高さ\(h\)[m]からトラックを落下させ、地面に落ちる時に速さが16.6… m/sとなる高さを求めていきます。
これは自由落下運動から、または力学的エネルギー保存を知ってる方はエネルギー保存から、高さ\(h\)を求めると、
\(h=14.22\) m
となりました。
つまり、速さ60キロのトラックに引かれるのは、トラックを高さ14 mから落とされるのと同じになります。
いかにトラックに引かれる衝撃がものすごいものかを理解していただけたと思います。
交通事故には気を付けてくださいね。
まとめ
今回は運動エネルギーの導出を仕事の考え方からやりました。
運動エネルギー自体は公式を覚えるだけですが、仕事を理解する上で、かなり勉強になったと思います。
難しく感じたら前回の記事『仕事で注意するべきポイントと仕事率についてわかりやすく解説します』を読んでから、再度この記事を読み直してくれたらと思います。
理解をあいまいにするのが一番ダメなので、必ず理解不足を解消してから、次の勉強に進んでください。
また、位置エネルギーとともに勉強するとエネルギーについていい勉強になります。
【合わせて読みたい】
重力による位置エネルギー
→重力による位置エネルギーとは??公式や運動エネルギーとの関係をわかりやすく解説します
弾性力による位置エネルギー
→弾性力による位置エネルギーとは??公式や運動エネルギーとの関係をわかりやすく解説します
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<


