こんにちは、ほーたです。
運動量と力積。
特に運動量保存則は、入試で頻出の単元です。
ここはどうしても理解したいところ。
僕自身運動量保存則が出来なくて、力学がほぼ全滅という経験があるので、
読み込んで、勉強してください。
運動量と力積の関係を理解し、運動量保存則を完全に使えるようにする。
目次
力積・運動量とは
力積と運動量
力積\(\vec{I}\)…力\(\vec{F}\)と力が働く時間\(\Delta t\)を掛け合わせたもの
$$\vec{I}=\vec{F}\times\Delta t$$
運動量\(\vec{P}\)…運動の勢いを表す量で、質量\(m\)と速度\(\vec{v}\)を掛け合わせたもの
$$\vec{P}=m\times\vec{v}$$
ここで注意してほしいことは、力積と運動量はベクトル量だということ。
つまりは、x軸とy軸の成分に分けれるということになります。
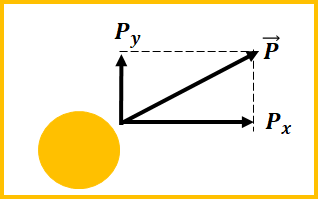
さて、ここで運動量と運動エネルギ―の違いって何??って思う人がいるでしょう。
大きな違いは二つあります。
それについて説明しようと思います。
運動量と運動エネルギーの違い
運動量と運動エネルギーのふたつの違い
- 運動量は力積を与える能力
運動エネルギーは仕事を与える能力 - 運動量はベクトル量
運動エネルギーは数値としての量
100 kg·m/s = 100 N·sの運動量を持つ物体は、100 N·sの力積を与える能力があり、
100 Jの運動エネルギーを持つ物体は、100 Jの仕事をする能力がある、ということです。
そして、x軸方向に\(v\)で進む物体には、
x軸方向に運動量\(m v\)を持ち、運動エネルギー\(\frac{1}{2}m v^2\)を持ち、
y軸方向に\(v\)で進む物体には、
y軸方向に運動量\(m v\)を持ち、運動エネルギー\(\frac{1}{2}m v^2\)を持つ。
このように、運動量は向きがあり、運動エネルギーは大きさだけを持ちます。
もう一度念押しするが、運動量はベクトル量。
これはマジで大事なことなので、しっかり覚えておきましょう。
力積と運動量の関係【公式・導出】
公式
物体が受けた力積\(\vec{I}\)=物体の運動量の変化\(\Delta\vec{P}\)
この公式を導出していきます。
導出
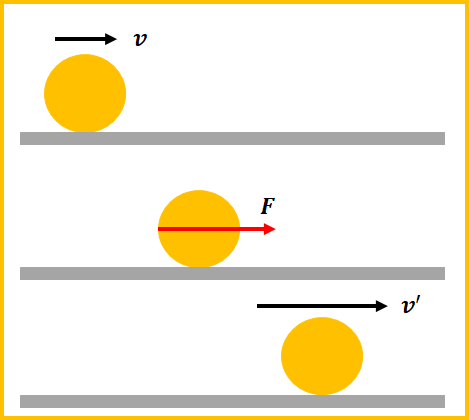
力学の基本の式「運動方程式」から導出していきます。
$$m\vec{a}=\vec{F}$$
加速度の定義を考えます。
$$\vec{a}=\frac{\vec{v}’-\vec{v}}{\Delta t}$$
これを運動方程式に代入。
$$\begin{align}m\vec{a}=&m\frac{\vec{v}’-\vec{v}}{\Delta t}=\vec{F}\\\\\Leftrightarrow&m(\vec{v}’-\vec{v})=\vec{F}\times\Delta t\\\\\Leftrightarrow&\Delta\vec{P}=\vec{I}\end{align}$$
これで公式が導出されました。
この公式からもうひとつわかる情報があります。
これが運動量保存則というものです。
これについて説明していきます。
運動量保存則【公式・導出】
公式
条件 : 物体の系の外部からの力(外力)が働かないとき
$$m\vec{v}+M\vec{V}=m\vec{v}’+M\vec{V}’$$
この公式を上の力積と運動量の関係式から導出します。
導出
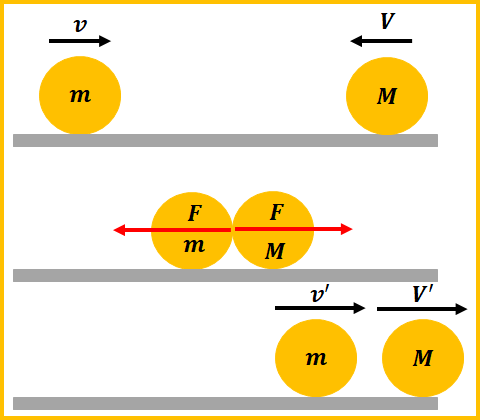
上に公式を書いているように外力が働ないときに成り立つ公式なので、
内力(物体間でのみで働く力)が働く場合に絞って導いていきます。
まず、それぞれの物体について力積と運動量の関係を考えます。
物体Aにつてい
$$m(\vec{v}’-\vec{v})=-\vec{F}\Delta t$$
物体Bについて
$$M(\vec{V}’-\vec{V})=\vec{F}\Delta t$$
この2式を足し合わせます。
$$\begin{align}&m(\vec{v}’-\vec{v})+M(\vec{V}’-\vec{V})=0\\\\\Leftrightarrow&m\vec{v}+M\vec{V}=m\vec{v}’+M\vec{V}’\end{align}$$
これで運動量保存則が導かれました。
それでは、運動保存則を用いた現象を考察して理解を深めていきます。
宇宙空間で移動する方法
あなたが宇宙空間にいるとします。
酸素は供給されてる状態、宇宙空間内でひとりで静止しています。
この時どうやって移動しますか??
5分間くらい考えてほしい。
------------------------
さて。運動量と力積を勉強したので想像は付くでしょう。
答えは、なにかを投げて運動量を与える、です。
そうすると、それを同じ運動量を投げた方向と真逆の方向に持ちます。
悟空がかめはめ波を撃つとき、かめはめ波と反対側に反動を受けるというイメージ。
このように物体を運動量を与えることで、その逆の方向に運動量を得られるということになります。
つまり、
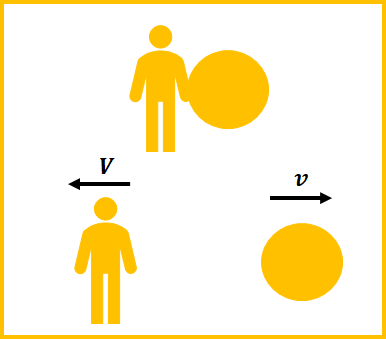
質量\(M\)の僕が、質量\(m\)の物体を速度\(\vec{v}\)で投げる時、
自分が速度\(-\vec{V}\)与えられるとします。
運動量保存則を立てます。
$$\begin{align}&m\times 0+M\times 0=m\times\vec{v}-M\times\vec{V}\\\\\Leftrightarrow&M\times\vec{V}=m\times\vec{v}\end{align}$$
ここから投げた向きと逆に運動量を得られます。
まとめ
このまとめを見て、記事の内容を説明できるまで反復しましょう。
力積と運動量(ベクトル量であることに注意)
力積 : \(\vec{I}=\vec{F}\times\Delta t\)
運動量 : \(\vec{P}=m\times\vec{v}\)
力積と運動量の関係
\(\vec{I}=\Delta\vec{P}\)
運動量保存則 : 外力が働かないときに成立
\(m\vec{v}+M\vec{V}=m\vec{v}’+M\vec{V}’\)
それでは。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<


