こんにちは、ほーたです。
力学的エネルギー、これは物理を学習していく上でかなり大切なパートです。
これが分からなければ、力学だけでなく電機分野でも解ける問題が限られてくるので、必ず理解するようにして下さい。
それでは解説していきます。
力学的エネルギーを完全に理解し、物理の土台を築く。
目次
保存力と非保存力とは
力学的エネルギーを考えるうえで保存力と非保存力は非常に重要です。
保存力とは、位置エネルギーを定義できる力のことです。
具体的には、重力と弾性力だと思ってくれればいいです。
そして非保存力とは、保存力以外の力のことです。
摩擦や垂直抗力がこれにあたります。
力学的エネルギー保存則とは
力学的エネルギーとは
力学的エネルギーとは、運動エネルギーの効果と、重力による位置エネルギーの効果と、弾性力による位置エネルギーの効果の足し合わせのことを言います。
つまり力学的エネルギーを\(E\)とすると、速さ\(v\)、基準地点からの高さ\(h\)、伸び縮み\(x\)によって、
$$E=\frac{1}{2}mv^2+mgh+\frac{1}{2}kx^2$$
になります。
$$E=\frac{1}{2}mv^2+mgh+\frac{1}{2}kx^2$$
運動エネルギー、重力による位置エネルギー、弾性力による位置エネルギーについては下記から読んでください。かなり重要な考え方も書いています。
【合わせて読みたい】
運動エネルギー
→運動エネルギーとは??公式の求め方から具体的な計算まで詳しく解説します
重力による位置エネルギー
→重力による位置エネルギーとは??公式や運動エネルギーとの関係をわかりやすく解説します
弾性力による位置エネルギー
→弾性力による位置エネルギーとは??公式や運動エネルギーとの関係をわかりやすく解説します
力学的エネルギー保存則とは
保存力のみが仕事をする状態では、力学的エネルギーが保存する法則します。
このことを力学的エネルギー保存則といいます。
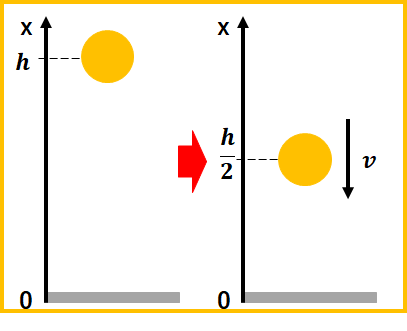
例えば、高さ\(h\)から物体を落としたときの力学的エネルギーは、保存力が働く状態では、高さが\(h/2\)の時の力学的エネルギーと等しくなるということです。
力学的エネルギー保存則の公式
上記のように保存力のみが仕事をする運動では力学的エネルギーが保存します。
最初の力学エネルギーを\(E\)、後の力学的エネルギーを\(E’\)とすると、
$$E=E’$$
と表せることになります。
具体的な証明方法は、保存力による仕事を計算することで証明できます。
詳しくは下記を順番に読むことで理解できます。
【合わせて読みたい】
- 運動エネルギーとは??公式の求め方から具体的な計算まで詳しく解説します
- 重力による位置エネルギーとは??公式や運動エネルギーとの関係をわかりやすく解説します
- 弾性力による位置エネルギーとは??公式や運動エネルギーとの関係をわかりやすく解説します
【超重要】非保存力が仕事をする場合の公式
保存力のみが働く運動では力学的エネルギー保存則が成り立つことが分かりましたが、非保存力が働く場合はどうでしょうか??
結論を言うと、非保存力に仕事をされた分、力学的エネルギーに変化があるということになります。
具体的に見ていきましょう。
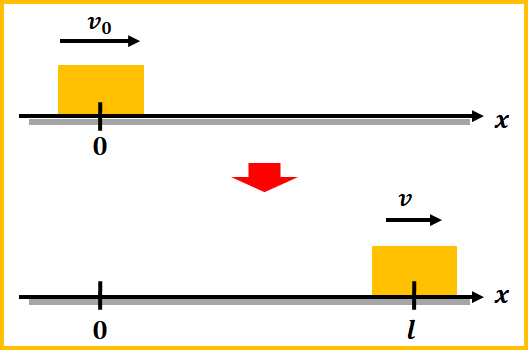
例えば、図のように、動摩擦係数が\(\mu’\)の粗い面上を質量\(m\)の物体が運動してる状況を考えます。
速度\(v_{0}\)から摩擦によって減速して、速度\(v\)になった時に、距離\(l\)だけ進んだとしましょう。
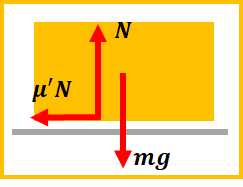
上図の力の作図から運動方程式を立てると以下のようになります。
$$ma=-\mu’mg$$
この時、図に従って、初期位置\(0\)、初速度\(v_{0}\)、加速度\(-\mu’g\)となるので、等加速度の公式は、
$$v^2-v_{0}^2=2a(x-x_{0})$$
より、
$$v^2-v_{0}^2=2(-\mu’g)l$$
となります。
両辺に\(m/2\)をかけます。
$$\frac{1}{2}mv^2-\frac{1}{2}mv_{0}^2=-\mu’mgl$$
これは
(力学的エネルギーの変化\(\Delta E\))=(非保存力がした仕事\(W\))
になります。
このように非保存力が働く場合は、
$$\Delta E=E-E’=W$$
と合わせます。
ここで注意してほしいのは、左辺の力学的エネルギーの変化\(\Delta E\)は、「(後の力学的エネルギー)-(前の力学的エネルギー)」ということです。
「後ー前」で覚えてください。
それでは公式をまとめていきます。
$$\begin{align}&力学的エネルギー保存則 : E=E’\\\\&非保存力が仕事する : \Delta E=W\end{align}$$
問題演習
問題
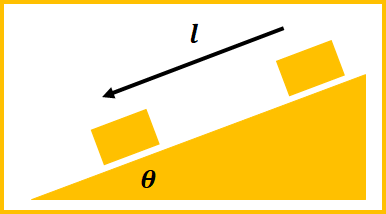
図のように、質量\(m\)の物体が傾き\(\theta\)の面に沿って、距離\(l\)だけ滑り下りる。このときの速度\(v\)を、物体が滑らかな面を滑る場合と動摩擦係数\(\mu’\)の面を滑るとき、の両方の場合で求めよ。
解答
まず滑らかな面を滑っているときの運動を考えましょう。
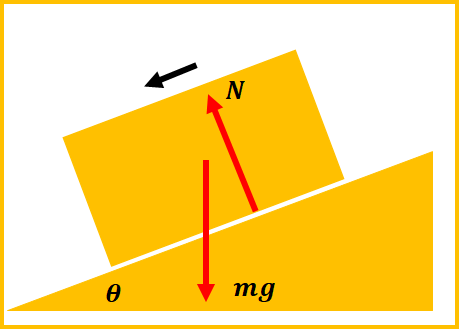
力の作図をすると非保存力による仕事がないので、力学的エネルギーが保存します。
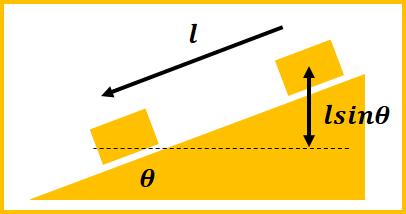
重力による位置エネルギーの基準値を\(l\)だけ滑り降りたときの位置だとすると、最初の物体の高さは\(lsin\theta\)になります。
よって、力学的エネルギー保存則より、以下が成り立ちます。
$$mg\times (l sin\theta)=\frac{1}{2}mv^2$$
ここから速度\(v\)が求まります。
$$v=\sqrt{2glsin\theta}$$
次に粗い面上を滑るときの運動を考えましょう。
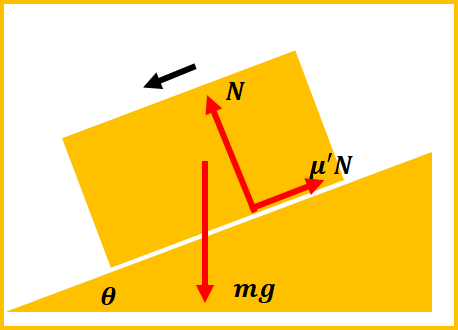
力の作図から非保存力が働くことが分かります。
y軸方向の力の作図から垂直抗力\(N\)は\(N=mg cos\theta\)になるので、動摩擦力\(f\)は\(f=\mu’mg cos\theta\)となります。
力学的エネルギーの考え方から「\(\Delta E=W\)」より、
$$\frac{1}{2}mv^2-mg l sin\theta=-(\mu’ mg cos\theta)\times l$$
が成り立ちます。
ここから
$$v=\sqrt{2gl(sin\theta-\mu’ cos\theta)}$$
と求まります。
【解答終】
まとめ
今回の重要なポイントは
- \(E=E’\)
- \(\Delta E=W\)
です。
これは本当に重要な考え方なので何回も読んで、必ず理解してください。
この記事を読んだ後にもう少し練習問題を解いて理解を深めてもいいかもです。
とにかく自分の身になるまで反復して学習してくださいね。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<