こんにちは、ほーたです。
今回は入試でめちゃめちゃ重要なフックの法則の考え方について説明します。
感覚的にフックの法則を使っている人は不意を突かれるとミスってしまうので、この記事でばねの問題が出たときの対処法を学んでくれればと思います。
考え方はすごい基本的なので、ここで基本的な考え方も身に着けてくれればと思います。
それでは解説していきます。
フックの法則の問題での正攻法を理解し、ばねの問題で迷わず解けるようにいする。さらに、合成ばね定数でこの考え方を実践する。
目次
弾性力とは
ばねを伸ばそうとすると縮もうとします、ばねを縮めようとすると伸びようとします。
このような元に戻ろうとする力を弾性力といいます。
だからばねに限らず輪ゴムやトランポリンにも弾性力は働いています。
フックの法則
ばねの弾性力の大きさ\(F\) [N]は、ばねの伸び縮みの大きさ\(x\) [m]に比例します。
これをフックの法則といいます。
$$F=kx$$
このとき、この比例定数\(k\) [N/m]をばね定数といいます。
単位からわかる通りばね定数は、ばねを1 m伸ばしたり縮めたりするのに必要な力ということが分かります。
つまり、ばね定数が大きいと伸び縮みしにくい硬いばねということが分かりますね。
フックの法則の問題を解くときの鉄則
さて、ここでフックの法則を考えるうえでの鉄則について説明していきましょう。
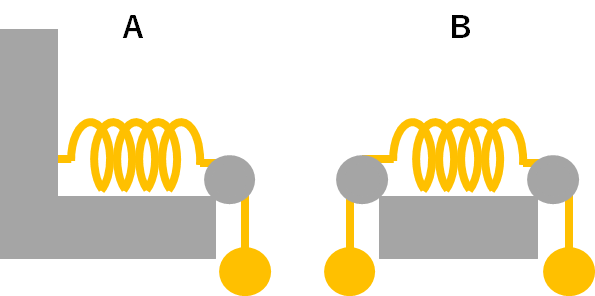
この図を見て感覚的にどちらのばねが伸びてそうですか??
Bのほうが両端に二つのおもりがついているので伸びそうと思う人が多いかもですね。
でも実際はどちらも同じ長さです。
これは感覚的に考えるとしくじるので必ず次に書いているように考えるようにしてください。
ばねの伸びを\(x\)として計算から伸びを求める。
図のようにつるされてるおもりの質量を\(m\)、AとBでのばねの伸びをそれぞれ\(x_{A}\)、\(x_{B}\)としましょう。
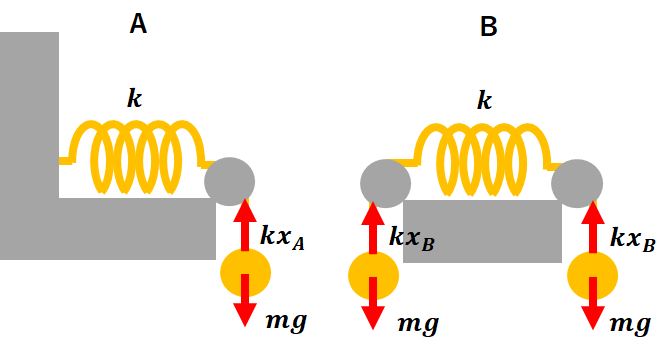
そうすると力のつり合いから、
$$Aについて : 0=k x_{A}-mg$$
$$Bについて : 0=k x_{B}-mg$$
となるので、これを解くと
$$x_{A}=\frac{mg}{k}$$
$$x_{B}=\frac{mg}{k}$$
となり、AとBで両方ともにばねの伸びが同じことが分かりますね。
こうやって考えることにより感覚で分からなくても理論的に正解が分かるということになります。
合成ばね定数の求め方:並列と直列でばね定数の公式
合成ばね定数とは複数のばね全体のばね定数です。
例えば、あとで説明する2つのばねを直列にする場合、2つのばね全体のばね定数を合成ばね定数といいます。
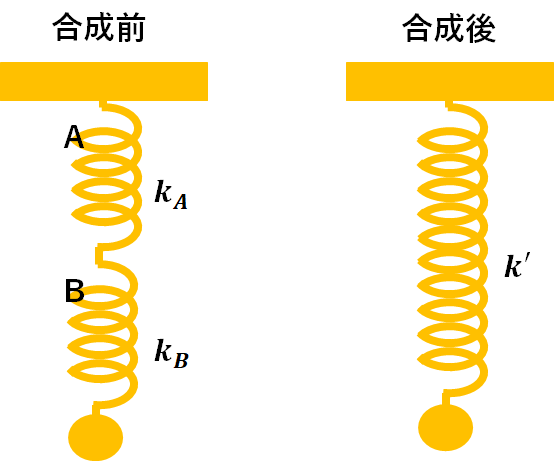
ばねを並列する場合でも同じように考えます。これについてもあとで説明しますね。
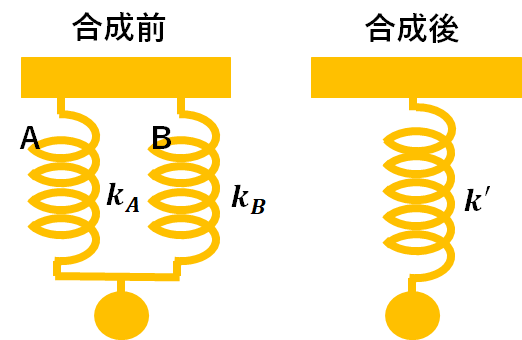
それでは、練習問題もかねて上記で説明したばねを並列と直列したときの合成ばね定数(二つ合わせたときのばね定数)を考えていきましょう。
これも上記のフックの法則の問題の考え方から導けます。
これに従って合成ばね定数を求めていきましょう。
ポイントは
- 物体での力のつり合いを立てる
- 合成ばね定数を用いて再度物体について力のつり合いを立てる
です。
直列つなぎの合成ばね定数
図のような体系を考えます。
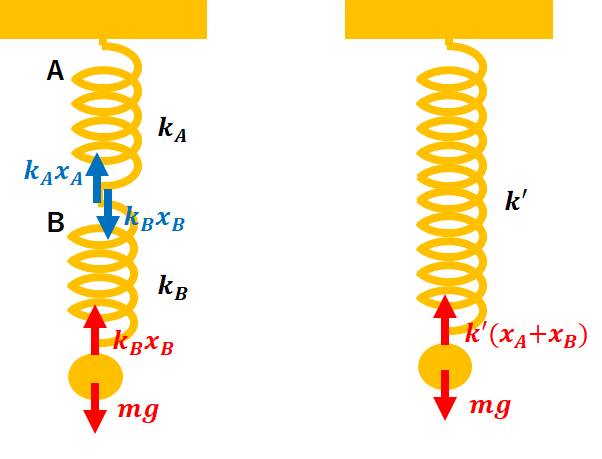
この体系について上記のポイントに従って問題を解いていきましょう。
1.物体についての力のつり合いを立てる
$$0=k_{B} x_{B}-mg$$
2.合成ばね定数を用いて、物体について力のつり合いを立てる。
全体のばねの伸びは\(x_{A}+x_{B}\)、合成ばね定数を\(k’\)とすると、働く力は\(k’\times(x_{A}+x_{B})\)となるので力のつり合いは、次のようになります。
$$0=k'(x_{A}+x_{B})-mg$$
3.ばねAとばねBの間で作用反作用を考える(これは直列の場合だけです。)
図の青い作図は、ばねBがばねAから受ける力が\(k_{A}x_{A}\)、ばねAがばねBから受ける力が\(k_{B}x_{B}\)だから、上向きに\(k_{A}x_{A}\)、下向きに\(k_{B}x_{B}\)が働きます。
$$k_{A} x_{A}=k_{B} x_{B}$$
ここで立てた3式から\(k’\)を求めると、
$$\frac{1}{k’}=\frac{1}{k_{A}}+\frac{1}{k_{B}}$$
が求まります。
これが2つのばねを直列につないだ時の合成ばね定数です。
並列つなぎの合成ばね定数
並列でも同じように考えていきましょう。
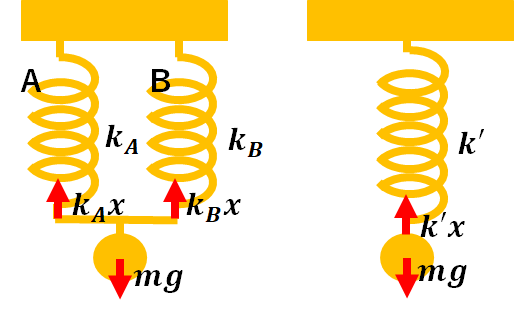
1.物体について力のつり合いを立てる。
$$0=k_{A} x+k_{B} x-mg$$
2.合成ばね定数を用いて力のつり合いを立てる。
全体のばねの伸びは\(x\)なので、合成ばね定数を\(k’\)とすると力のつり合いは次のようになります。
$$0=k’ x-mg$$
この2式から合成ばね定数を求めると
$$k’=k_{A}+k_{B}$$
と求められます。
それでは合成ばね定数をまとめましょう。
これは知っていても損はないので頭に入れておくくらいにするといいですね。
直列 : \(\frac{1}{k’}=\frac{1}{k_{a}}+\frac{1}{k_{B}}\)
並列 : \(k’=k_{A}+k_{B}\)
ここからばねを直列につなげるとばね定数が小さくなり、ばねを並列につなげるとばね定数が大きくなることが分かります。
同じばね定数のばねを直列つなぎすると合成ばね定数が\(k/2\)と半分になり、並列つなぎをすると合成ばね定数が\(2k\)となり二倍になります。
そして同じばね定数のばねを直列するか並列するかで合成ばね定数が4倍も変わるということが分かります。
【捕捉】サンドイッチ型の合成ばね定数
サンドイッチ型とは図のように二つのばねに物体が挟まれている状態です。
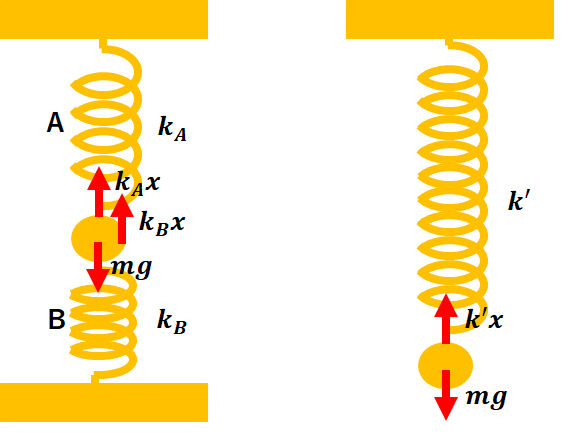
これはAが\(x\)だけ伸びて、Bが\(x\)だけ縮んでいる状態です。
それでは合成ばね定数を考えてみましょう。
1.物体においての力のつり合い
$$0=k_{A}x+k_{B}x-mg$$
2.合成ばねを用いた物体での力のつり合い
ここでも物体Aは元の位置から\(x\)だけずれているので全体のばねは\(x\)だけ伸びていることになります。
$$0=k’x-mg$$
この2式から\(k’\)を求めると、
$$k’=k_{A}+k_{B}$$
となることが分かる。
つまりばねを並列したときと同じ合成定数になります。
まとめ
いかがだったでしょうか??
今回はフックの法則の考え方を用いて合成ばね定数を求める問題演習をしました。
考え方としてはかなり基本的なことしかしてないのですが、少し複雑だったので難しく感じた方も多いかもしれません。
ですが何度も読んで手を動かすことで理解できるようになるので必ず理解するようにしてください。
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<


