こんにちは、ほーたです。
今回は自由落下運動について解説します。
物理を学習し始めて最初の具体的な運動で少し戸惑う人もいるかと思うが、
ここで踏ん張り理解して次のステップに進むことが物理を学習するうえで大切です。
分からないことを作ったまま、次の単元に行くことほど危ないことはありません。
しっかり理解していきましょう。
自由落下運動の公式を等加速度運動の式から導けるようになる。
目次
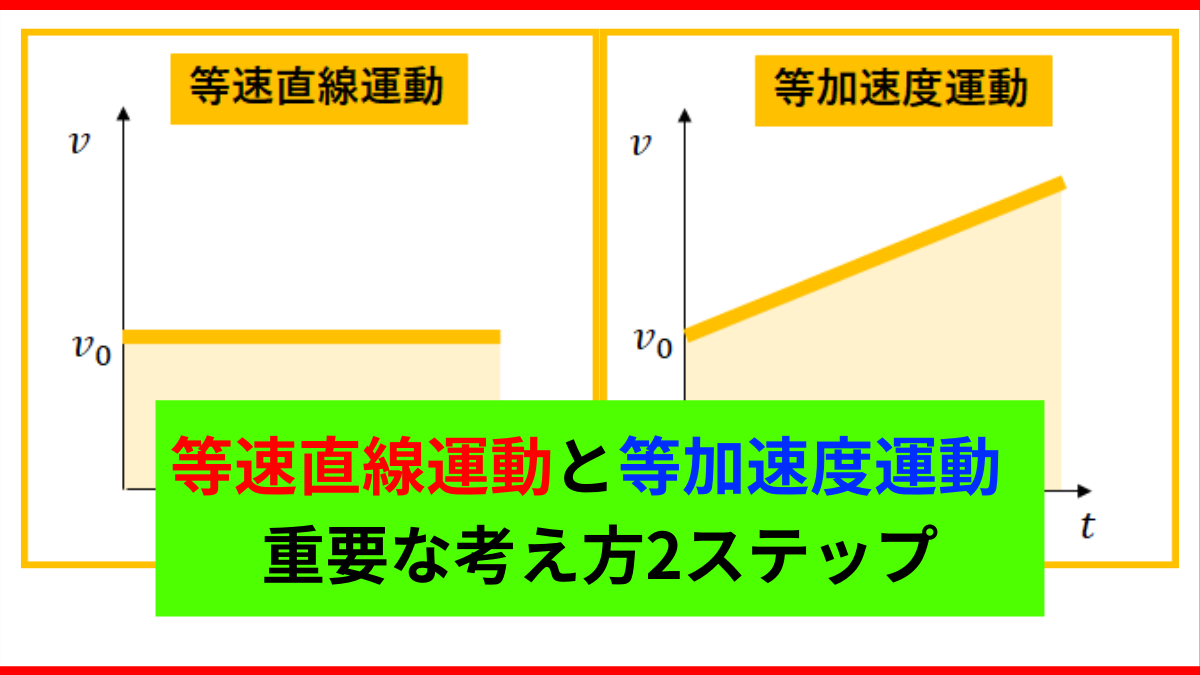
自由落下運動を考える上でのポイント
自由落下運動を考える時のポイントは等加速度運動だということです。
等加速度運動の公式から考えれば良い、ということになります。
ここが本当に大切です。
速度 : \(v=v_{0}+at\)
位置 : \(x=x_{0}+v_{0}t+\frac{1}{2}at^2\)
この式に等加速度運動の考え方
- 軸の決定
- 初期位置\(x_{0}\)、初速度\(v_{0}\)、加速度aの整理
で公式を導いていきます。
この順番について詳しくは下記の記事に書いているので、こちらを参考にしてください。
【合わせて読みたい記事】
自由落下運動の公式
等加速度運動の代表例が落体の運動。
落体とは重力のみを受けて空中を動く物体のことです。
この時の加速度を重力加速度といい、\(g=9.8 m/s^2\)の大きさです。
自由落下運動とは
落体の運動の中でも特に初速度0で落下する物体の運動のことをを自由落下運動といいます。
そしてこの自由落下運動は落下をし始めた位置を原点として鉛直下向きにx軸をとることで公式を導出します。
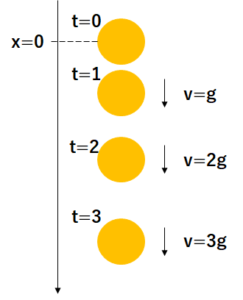
自由落下の速度の公式
まずは速度の公式からです。
自由落下運動は初期位置が0、初速度が0で加速度が重力加速度\(g\)になるので、
等加速度運動の公式において初速度と加速度をそれぞれ\(v_{0}=0\)、\(a=g\)とすることで求められます。
$$v=gt$$
これが自由落下運動の速度の公式。
これを覚えるのではなく等加速度運動の公式から導けるようにしてください。
自由落下の位置の公式
次に位置の公式。
これも等加速度運動の公式を使って簡単に導けます。
自由落下運動の条件は初期位置、初速度と加速度がそれぞれ\(x_{0}=0\)、\(v_{0}=0\)、\(a=g\)なので、これを代入していきます。
$$x=\frac{1}{2}gt^2$$
これが自由落下の位置の公式。
これも速度と同様に導けることが大切です。
速度 : \(v=gt\)
位置 : \(x=\frac{1}{2}gt^2\)
自由落下運動を初期条件を変えて考える
少し問題を解いていきましょう。
問題

物体を高さ\(h\)から落とすとする。この時地面に落下するときの速度を求めよ。ただし、軸は図に書いてある通りに設定するものとする。また、重力加速度は\(g\)とする。
解答
等加速度運動の考え方に従って考えていきます。
まず、軸の決定ですが、これは問題文で指定されているので不要ですね。
次に、初期条件(初期位置、初速度、加速度)を求めていきます。
今回の問題では、初期条件が初期位置\(h\)、初速度\(0\)、加速度\(-g\)。
(重力加速度も向きが軸の向きに逆向きになるので、負になることに注意)
それでは、等加速度運動の式を立てます。
$$v=-gt$$
$$x=h-\frac{1}{2}gt^2$$
ここから、落下するとき(\(x=0\))の時刻\(t_{0}\)を求めると、
$$0=h-\frac{1}{2}gt_{0}^2$$
より、
$$t_{0}=\sqrt{\frac{2h}{g}}$$
となります。
落下したときの速度\(v_{1}\)は、
$$v_{1}=-gt_{0}=-\sqrt{2 h g}$$
と求まりました。【終】
まとめ
このまとめを見て、記事の内容を説明できるまで反復しましょう。
自由落下運動の公式
速度 : \(v=g t\)
位置 : \(x=\frac{1}{2}gt^2\)
それでは。
【合わせて読みたい】
オリジナルテキストを無料でプレゼントします
僕は受験生の時、物理の偏差値を80近くまで伸ばし、京大模試で1桁を取り、京都大学に合格しました。
しかし、これは順調に伸びたのではなく、あるコツをつかむことが出来たからです。
その一番のきっかけになったのを力学の考え方にまとめました。
力学の基本中の基本です。
色々な問題に応用が効きますし、今でも僕はこのやり方に沿って問題を解きます。
無料配布中です。
>>>詳しくはこちらをクリック!<<<
もしくは、下記画像をクリック!

>>>力学の考え方を受け取る<<<